Распад - произвольный разрыв
Cтраница 3
В данном издании в первую главу включен дополнительно параграф, посвященный решению классической задачи о распаде произвольного разрыва. Это решение использовано в дальнейшем в качестве теста. [31]
При этом оказывается, что численный поток в схеме Роу определяется по точному решению задачи о распаде произвольного разрыва для таким образом линеаризованной системы уравнений. [32]
Усредненные по времени потоки могут быть найдены, например, с использованием приближенного решения задачи о распаде произвольного разрыва между параметрами в смежных ячейках с помощью метода Роу. Процедура становится в особенности простой, если в (5.7.10) - (5.7.12) интегралы по времени вычисляются с первым порядком точности, используя величины с нижнего временного слоя. [33]
Как известно, в схеме Годунова по параметрам в соседних ячейках сначала решаются вспомогательные задачи о распаде произвольного разрыва. Так как конфигурация сетки в момент t т определяется положением узлов ударной волны на направляющих, то ее построение состоит в определении смещений узлов, а не смещений центров прямолинейных отрезков, составляющих волну. [34]
Если первоначальная поверхность криволинейна, а начальные распределения параметров не однородны и не одномерны, то полученное описание распада произвольного разрыва может применяться аишь локально в окрестности каждой точки и лишь в течение малого промежутка времени. При этом конфигурация образующихся первоначально волн может быть различной вблизи разных участков начального разрыва. [35]
 |
Различные случаи распада произвольного разрыва в инертном газе. [36] |
Более сложный случай имеет место, когда справа от поверхности разрыва находится горючая смесь, так что при распаде произвольного разрыва по ней может пойти фронт пламени. [37]
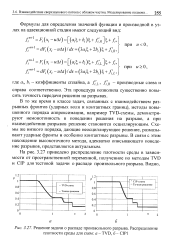 |
Решение задачи о распаде произвольного разрыва. Распределение плотности среды для схем. а - TVD, б - CIP1. [38] |
На рис. 3.27 приведено распределение плотности среды в зависимости от пространственной переменной, полученное по методам TVD и CIP для тестовой задачи о распаде произвольного разрыва. [39]
Для того чтобы определить новую структуру решения, возникающую при взаимодействии разрывов, и получить начальные условия для продолжения счета при, следует воспользоваться известным решением задачи о распаде произвольного разрыва. При этом в соответствии с новой структурой решения следует заново разбить расчетную область на области непрерывности, построить новую расчетную сетку и внести соответствующие изменения в подпрограммы для расчета границ частичных областей. [40]
Методы с выделением разрывов ( Годунов и др., 1961, 1979; Крайко и др., 1980; По-тапкин, 1983), которые основаны на точных формулах распада произвольного разрыва, не проявляют особой чувствительности к способу вычисления скоростей на фронте выделяемого разрыва. В отличие от них метод самоподстраивающихся подвижных сеток, основанный на приближенном решении задачи Римана по методу Роу, заметно зависит от алгоритма вычисления скоростей. Однако при этом такой метод является методом сквозного счета, а вычисление скоростей подвижных сеток проводится отдельной независимой процедурой. Для точного улавливания и выделения разрыва самоподстраивающимися сетками оказалось удачным использование предельной реконструкции, которая позволяет вычислять распределение скоростей вдоль фронта разрыва с требуемой точностью. [41]
Последнее соотношение (13.155) выполняется вдоль траектории движения частиц среды и позволяет получить связь между давлением и плотностью в газообразных продуктах детонации и жидкости на контактной поверхности в последовательные моменты времени, а также решить задачу о распаде произвольного разрыва при выходе ДВ на поверхность заряда. [42]
Эта аппроксимация позволяет применить ранее найденные формулы точного распада произвольного газодинамического разрыва. После этого используются формулы точного распада произвольного разрыва для двучленного УРС. Такая аппроксимация применяется как для одного газа, так и для двух контактирующих газов со своими собственными УРС. [43]
Движение, возникающее после образования произвольного разрыва, мы называем обыкновенным взрывом. Обыкновенный взрыв называют также распадом произвольного разрыва. В газе произвольный разрыв не сохраняется, а происходит мгновенное выравнивание давления и скоростей по частицам контактирующей поверхности. Но указанные частицы обоих газов, как будет показано ниже, образуют поверхность разрыва плотностей и температур. Так как эта поверхность разрыва находится на одних и тех же частицах газа, то ее называют волной стационарного разрыва. Скорость распространения волны стационарного разрыва, очевидно, совпадает со скоростью частиц. [44]
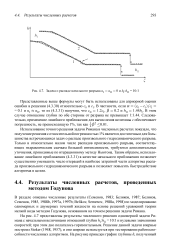 |
Задача о распаде начального разрыва и и 0 и / Zp / zn. [45] |
Страницы: 1 2 3 4