Распределение - комплексная амплитуда
Cтраница 1
Распределение комплексной амплитуды на опорной сферической поверхности F ( и) в пространстве предметов свертывается в распределение амплитуды на опорной сферической поверхности F () в пространстве изображений. [1]
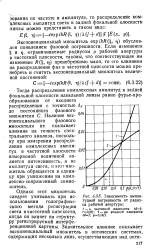 |
Зависимость амплитудной погрешности от радиуса рабочей апертуры. [2] |
Тогда распределение комплексных амплитуд в задней фокальной плоскости идеальной линзы равно фурье-пре-образованию от входного распределения с точностью Аа до постоянного фазового множителя С. [3]
Если распределение комплексных амплитуд на объекте описывает некоторая функция Q ( х, у), то 2 ( л 0) у) будет характеризовать распределение амплитуд поля на том изображении, которое должно быть получено по законам геометрической оптики. [4]
 |
Эквивалентная безлинзовая голограмма Фурье. [5] |
Эти выражения описывают распределение комплексных амплитуд в продифрагировавшей на голограмме волне непосредственно за голограммой, когда она освещается плоской волной единичной амплитуды при условии, что параметры голографической записи выбраны надлежащим образом. [6]
Для регистрации этого распределения комплексных амплитуд света голографическим методом с помощью зеркала 32 и полупрозрачного зеркала ПП32 на фотопластинку под углом 0 направляют плоскую опорную волну. [7]
Сохраняется и вид распределения комплексной амплитуды на опорных поверхностях, которые остаются сферическими. Изменяются только радиусы кривизны р последних и, вместе с w, масштабы распределений, причем у всех пучков одинаково - точно так же, как у простейшего из них гауссова. Отсюда ясно, что, скажем, рис. 1.6 может быть в равной степени отнесен к любым эрмитовым и лагерровым пучкам с теми же р и w, только картина распределения, для которой н задает масштаб, у каждого пучка своя. [8]
Как видно из (6.3.1), распределение комплексных амплитуд света в плоскостях Р2 и PI отличается от соотношения, определяемого точным фурье-преобразова-нием, на величину, определяемую выражением, стоящим в квадратных скобках. Очевидно, что для получения точного фурье-преобразования необходимо, чтобы эта величина была значительно меньше единицы. Величина, стоящая в квадратных скобках в (6.3.1), является весовым коэффициентом, который изменяет вклад каждой точки х, у плоскости Pi, вносимый в формирование результирующей амплитуды в точке, т) плоскости РЧ. Этот весовой коэффициент учитывает влияние изменения оптического пути и коэффициента наклона для рассматриваемых точек. Обычно этим влиянием пренебрегают, полагая, что необходимое условие выполнено. [9]
Однако для некоторых случаев особый интерес представляют распределения комплексной амплитуды и интенсивности сканирующего пятна. [10]
 |
Структурная схема устройства оптической обработки изображений, использующего модулятор типа Lumatron. [11] |
Результат вычисления представляет собой световую картину, распределение комплексных амплитуд в которой связано с распределением амплитуд на входе определенным соотношением. [12]
На голограммах Фурье записывается интерференция двух волн, распределение комплексных амплитуд которых в плоскости голограммы представляет собой фурье-образы распределений комплексных амплитуд как объекта, так и опорного источника. При этом опорный источник должен находиться в той же плоскости, что и объект. Следовательно, объект должен быть по существу плоским или по крайней мере его толщина должна быть меньше, чем расстояние от объекта до линзы. Линза применяется для того, чтобы получить фурье-образ распределений комплексных амплитуд как объекта, так и опорного точечного источника. Голограмма формируется в задней фокальной плоскости линзы. [13]
Наиболее полную информацию о точечном изображении дает функция распределения комплексной амплитуды, получаемая с помощью интеграла Френеля - Кирхгофа на основе волнового фронта, формируемого оптической системой в ее выходном зрачке. Первая представляет собой распределение интенсивности света в точечном изображении. [14]
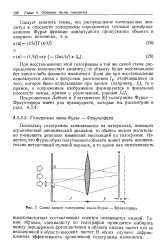 |
Схема записи голограммы квази - Фурье - Фраунгофера. [15] |
Страницы: 1 2 3 4