Распределение - комплексная амплитуда
Cтраница 2
При восстановлении этой голограммы в той же самой схеме распределение комплексных амплитуд по объекту будет восстановлено без какого-либо фазового множителя. [16]
В системе гетеродинного сканирования [120, 121] сфокусированный опорный пучок сканирует распределение комплексных амплитуд сигнальной волны, при этом результирующая интенсивность света, а следовательно, и выходной сигнал в каждой сканируемой точке определяется разностью фаз между сигнальной и опорной волнами в этой точке. [17]
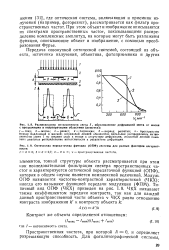 |
Оптическая передаточная функция ( ОПФ системы для разных факторов когерентности. [18] |
При этом объект и изображение описываются их спектрами пространственных частот, показывающими распределение комплексных амплитуд, на которые могут быть разложены функции, описывающие объект и изображение, с помощью преобразования Фурье. [19]
Выбор размеров и особенно формы входного зрачка позволяет в широких пределах управлять распределением комплексной амплитуды и наглядно выявить такие эффекты, связанные с тонкой структурой индивидуальных спеклов, как осцилляция видности интерференционных полос, их сдвиг на половину периода при переходе через нуль видности, визуализация функции пространственной когерентности спекл-поля. [20]
Полагая / i / 2 и считая ориентацию изображения несущественной, получаем для распределения комплексных амплитуд объектного пучка в плоскости сфокусированной голограммы выражение, не содержащее фазового множителя сферической волны. [21]
Как было сказано выше, поперечные моды лазерного излучения представляют собой пучки света, распределение комплексной амплитуды в сечении которых описывается собственными функциями оператора распространения в соответствующей среде. Фундаментальным свойством мод является сохранение структуры и ортогональности распространении в среде. [22]
Из сказанного должно быть ясно, что в таких случаях задачи о дифракционном преобразовании распределения комплексной амплитуды и об изменении состояния поляризация по прохождении сложной оптической системы могут рассматриваться независимо друг от друга. С методами решения первой мы уже ознакомились; анализ поляризационных харак-теристик когерентных пучков удобнее всего производить методом Джонса. [23]
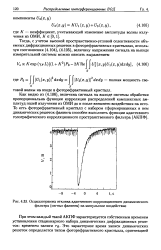 |
Осциллограмма отклика адаптивного корреляционного динамического фильтра ( сигнал фанинга на импульсное воздействие. [24] |
Как видно из (4.106), величина сигнала на выходе системы обработки пропорциональна функции корреляции распределений комплексных амплитуд полей излучения из ОМИ до и после внешнего воздействия на него. [25]
Прозрачный объект, являющийся источником возмущений, освещается идеальной плоской волной; после его прохождения распределение комплексной амплитуды волны приобретает вид и о егф, где ф - зависящие от поперечных координат фазовые отклонения, к-рые и подлежат регистрации. [26]
Нетрудно видеть, что в таком приближении прохождению волны через обычную диафрагму соответствует операция умножения распределения комплексной амплитуды в плоскости диафрагмы на вещественную функцию пропускания Т, равную единице на площади отверстия и нулю вне его. Среди них особую роль в теории играют так называемые гауссовые диафрагмы. [27]
На голограммах Фурье записывается интерференция двух волн, распределение комплексных амплитуд которых в плоскости голограммы представляет собой фурье-образы распределений комплексных амплитуд как объекта, так и опорного источника. При этом опорный источник должен находиться в той же плоскости, что и объект. Следовательно, объект должен быть по существу плоским или по крайней мере его толщина должна быть меньше, чем расстояние от объекта до линзы. Линза применяется для того, чтобы получить фурье-образ распределений комплексных амплитуд как объекта, так и опорного точечного источника. Голограмма формируется в задней фокальной плоскости линзы. [28]
Пусть тот из пучков, который на рис. 2.2 д следует от левого зеркала к правому, имеет на этой плоскости распределение комплексной амплитуды 11 т ( xi У J знания этого распределения, о. [29]
Следует отметить, что визуализация посредством регистрации распределения видности функции поперечной когерентности спекл-поля является наглядным образом, отражающим к тому же распределение комплексной амплитуды в индивидуальном спекле при выборе той или иной формы зрачка изображающей системы или самого диффузно рассеивающего объекта. [30]
Страницы: 1 2 3 4