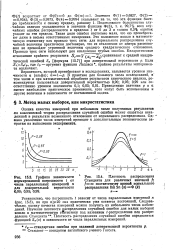
Распределение - случайная ошибка
Cтраница 2
Анализ промысловых данных испытания показывает, что наблюдающиеся распределения случайных ошибок измерения согласуются с нормальным законом распределения вероятностей. [16]
Точность измерений характеризуется величиной а - стандартом распределения случайных ошибок измерения. [17]
На практике чаще всего имеет место нормальный закон распределения случайных ошибок. В этом случае оценкой точности, характеризующей воспроизводимость результатов рент-геноспектрального анализа, является среднеквадратичная погрешность а, называемая также стандартным отклонением и определяемая как корень квадратный из дисперсии. Чем выше воспроизводимость анализа, тем меньшее и тем ближе отдельные результаты анализа к своему среднему значению, а - это абсолютная погрешность и поэтому характеризует возможную ошибку только при данном конкретном значении результата. [18]
Если результаты эксперимента вызывают сомнение в нормальности закона распределения случайных ошибок, то для решения вопроса о пригодности или непригодности нормального закона распределения надо произвести достаточно большое число измерений и применить один из описанных ниже критериев. [19]
Повторяя измерения большое число раз, можно установить закон распределения случайных ошибок. [20]
Для задач, которые возникают на практике, закон распределения случайных ошибок не известен и, строго говоря, он должен изменяться при переходе от одного случая к другому. Экспериментальное установление этого закона в каждом случае в принципе хотя и возможно, но требует проведения очень большого количества измерений. [21]
Если случайные ошибки удовлетворяют постулату Гаусса1), то законом распределения случайных ошибок является нормальный закон. [22]
Оценка качества измерений при небольшом числе полученных результатов яо классической теории распределения случайной ошибки может оказаться ненадежной в результате возможного отклонения от нормального распределения. Од-яако увеличение числа измерений, приводит к дополнительным экономическим затратам на выполнение эксперимента. [24]
В следующей главе будет выведен тот же закон из основного свойства распределения случайных ошибок. Он носит название нормального. Сейчас представим его лишь как частный случай той интерполяции биномиального закона, которая в общем виде приводит к гамма-распределению. [25]
В тех случаях ( см. выше), когда требуется исследовать закон распределения случайных ошибок измерения, поступают следующим образом. [26]
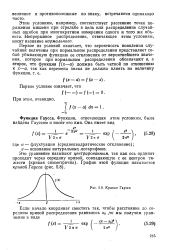 |
Кривая Гауоса. [27] |
Этим условиям, например, соответствует рассеяние точек поражения мишени при стрельбе в цель или распределение случайных ошибок при многократном измерении одного и того же объекта. [28]
Основными задачами теории случайных ошибок являются: нахождение наиболее вероятного значения результата и рациональная оценка величины и распределения случайных ошибок. [29]
При этом, учитывая обычно наблюдающуюся симметрию положительных и отрицательных случайных ошибок, принимают еще, что центр распределения случайных ошибок равен нулю. [30]
Страницы: 1 2 3 4