Распределение - случайная ошибка
Cтраница 1
Распределение случайных ошибок во многих видах физических измерений является распределением Гаусса, или нормальным распределением. [1]
Если распределение случайных ошибок для обоих методов близко к нормальному, сопоставление выборочных дисперсий сводится к нахождению отношения большей дисперсии к меньшей. В случае правильности предположения, что генеральные дисперсии у обоих методов одинаковы, это отношение распределено как F - Фишера. [2]
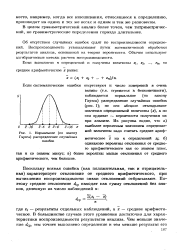 |
Нормальное ( по закону. [3] |
Гаусса) распределение случайных ошибок ( рис. 1); по оси абсцисс откладывают значения определяемой величины (), а по оси ординат - вероятности получения их при анализе. [4]
При этом распределение случайных ошибок симметрично относительно нуля: ошибки, противоположные по знаку, но равные по абсолютной величине, встречаются одинаково часто. Из симметрии распределения ошибок следует, что истинный результат наблюдения есть математическое ожидание соответствующей случайной величины. [5]
Из симметричности распределения случайных ошибок вытекает важный вывод: при отсутствии систематических и грубых ошибок истинный результат наблюдения есть математическое ожидание соответствующей случайной величины. В связи с этим особую важность приобретает проблема освобождения результатов наблюдений от всех систематических и грубых ошибок. [6]
Исследовать закон распределения случайных ошибок измерений в подобном случае не обязательно. [7]
Заметим, что распределение случайных ошибок Wk неизвестно. [8]
Переходим к выводу распределения случайных ошибок и примем давно установившуюся в теории ошибок схему, согласно которой все случайные ошибки, зависящие от очень большого числа малозначащих факторов, можно представить суммами чрезвычайно малых элементарных ошибок. Поскольку малость этих гипотетических элементов чисто условная и ничем не может быть ограничена, то в дальнейшем мы имеем право считать их бесконечно малыми, а в пределе в надлежащих случаях даже приравнивать к нулю. Кроме того, ничто не мешает нам принимать эти ошибки равными. Такое дололнительное упрощение к схеме элементарных ошибок, введенное Хагеном, делает весь вывод более наглядным и более простым, а поэтому в дальнейшем мы его используем. [9]
Гауссом был найден закон распределения случайных ошибок. Этот закон справедлив почти для любых измерений, в том числе и для количественного спектрального анализа. На рис. 135, а графически показана зависимость числа измерений, в которых встречается та или иная ошибка, от ее величины при достаточно большом числе измерений. [10]
 |
Кривая нормального распределения ошибок ( N - число измерений с данной ошибкой. е - ошибка единичного измерения.| Кривые нормального. [11] |
На рис. 7 приведена кривая распределения случайных ошибок, построенная по очень большому количеству параллельных определений. Ее называют кривой нормального распределения ошибок или кривой Гаусса. Она характерна для большинства конкретных аналитических методик. [12]
Установим аналитическое выражение для закона распределения случайных ошибок измерений. [13]
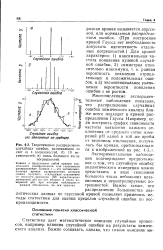 |
Теоретическое распределение случайных ошибок, возникающих за счет а 4 погрешностей, б 10 погрешностей, в очень большого числа погрешностей. [14] |
Многочисленные экспериментальные наблюдения показали, что распределение случайных ошибок химического анализа ближе всего подходит к кривой распределения Гаусса. Например, если построить график зависимости частоты появления каждого отклонения от среднего сотни измерений рН одной и той же пробы от величины отклонения, получилась бы кривая, приближающаяся к изображенной на рис. 4 - 3, г. Экспериментальные наблюдения подтверждают предположение о том, что случайную ошибку аналитического измерения можно представить в виде скопления большого числа небольших независимых и неконтролируемых погрешностей. Важно также, что распределение большинства аналитических данных по гауссовой кривой позволяет применить методы статистики для оценки пределов случайной ошибки по воспроизводимости. [15]
Страницы: 1 2 3 4