Распределение - плотность - вероятность
Cтраница 1
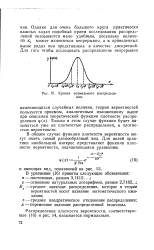 |
Кривая нормального распределения. [1] |
Распределение плотности вероятности, соответствующее ( 16) и рис. 14, называется нормальным. [2]
Распределение плотности вероятности в этом случае зависит не только от значения случайной погрешности А, но и от числа п наблюдений. [3]
Распределение плотностей вероятностей при первом значении соответствует наиболее неблагоприятному сочетанию параметров, а при втором - максимально благоприятному. [4]
Распределение плотности вероятности р ( К) является бимодальным и, по образному выражению И. [5]
Распределение плотности вероятности случайной величины для средней стадии закачки топлива в резервуар не соответствует ни одной из рассмотренных гипотез. [6]
Распределение плотности вероятности погрешности квантования для i - ro кванта ш ( Дки у) определяется распределением вероятности квантуемой величины. [7]
Это распределение плотностей вероятностей называется распределением Гаусса. [8]
Графически распределения плотности вероятности (12.9), (12.13) и (12.14) представлены на фиг. [9]
Кривая распределения плотности вероятностей по закону эксцентриситета ( рис. 1.16) несимметрична. [11]
Изменение распределения плотности вероятностей в зависимости от условной цены, начиная для некоторого момента времени, представлено на рис. 17.5. Из зависимости между плотностью вероятностей и вероятностью (17.1) вытекает, что для одной и той же цены вероятность будет различной в разные моменты времени. [12]
Изменение распределения плотности вероятностей в зависимости от условной цены, начиная для некоторого момента времени, представлено на рис. 17.5. Из зависимости между плотностью вероятностей и вероятностью (17.1) вытекает, что для одной и той же цены вероятность будет различной в разные моменты времени. [13]
 |
Эволюция плотности распределения вероятностей погрешности ТСХ с учетом погрешности квантования. [14] |
Закон распределения плотности вероятности суммарной погрешности в этом случае определяется композицией законов распределения ее составляющих - равномерного и нормального для случая определения моментов времени, треугольного распределения Симпсона и нормального распределения Гаусса для случая измерения интервалов времени. Указанные композиции могут быть найдены с помощью регулярных методов теории вероятностей. [15]
Страницы: 1 2 3 4
