Распределение - плотность - вероятность
Cтраница 3
Фурье, показателя Ляпунова, распределения плотности вероятности, фрактальной размерности. [31]
Другой важнейшей величиной, характеризующей распределения плотностей вероятностей, является о - стандартное рассеяние ( вариация, среднеквадратичное отклонение) переменной. [32]
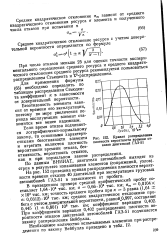
На рис. 4.22 показан пример распределения плотности вероятности для хаотических колебаний изогнутого стержня. [33]
 |
Кривая распределения плотности вероятности времени отказов двигателей ГАЗ-51. [34] |
На рис. 152 приведена кривая распределения плотности вероятности времени отказов 40 двигателей при эксплуатации грузовых автомобилей ГАЗ-51 в зависимости от пробега. [35]
 |
Определение плотности вероятности.| Распределение случайной величины X, заданной в виде гистограммы вероятностей интервалов. [36] |
На рис. 1, е приведено распределение плотности вероятности, которое получается из гистогра. [37]
Они свидетельствуют о том, что распределение плотности вероятностей концентрации в несжимаемой жидкости и в среде переменной плотности заметно различаются. Расчеты средней плотности, проведенные с использованием решения уравнения для P ( z) и аппроксимаций для P ( z) из [2,3], в которых влияние переменности плотности не учитывалось, показали значительное расхождение. [38]
Это указывает на вероятную возможность расчета распределений плотности вероятности для детерминированных хаотических систем методами теории случайных колебаний. [39]
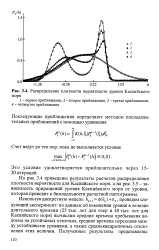 |
Распределение плотности вероятности уровня Каспийского моря. [40] |
На рис. 3.4 приведены результаты расчетов распределения плотности вероятности для Каспийского моря, а на рис. 3.5 - зависимость приращений уровня Каспийского моря от уровня, которая приводит к бимодальности расчетной гистограммы. [41]
ЛИУВЙЛЛЯ УРАВНЕНИЕ - ур-ние для ф-ции распределения плотности вероятности частиц в фазовом пространстве - основное ур-ние статистич. [42]
При аддитивной погрешности и равномерном законе распределения плотностей вероятностей параметров сравниваемых величин число различимых значений информационного параметра на входе компаратора ( см. рис. 2.12, о) практически обратно пропорционально погрешности. [43]
При аддитивной погрешности и равномерном законе распределения плотностей вероятностей параметров сравниваемых величин число различимых значений информационного параметра на входе компаратора ( см. рис. 2.12, а) практически обратно пропорционально погрешности. [44]
Для того чтобы получить представление о распределении плотности вероятности ошибки, которая вносится апроксимацией уравнения статической характеристики прямолинейной зависимостью, обратимся к фиг. [45]
Страницы: 1 2 3 4