Выборочное распределение

Cтраница 1

Выборочное распределение: в табл. F содержатся критические значения R для п 20 и л2 20 при а 0 05 и двустороннем критерии. [1]

Выборочное распределение: при больших выборках распределение z примерно соответствует нормальному. [2]

Выборочное распределение: поскольку N ( число пар) не превышает 50, то для проверки Н0 можно воспользоваться табличными значениями биномиальной переменной. [3]

Выборочное распределение часто используется, когда экстенсивное распределение нежелательно или не требуется, а исключительное распределение не обеспечивает необходимый охват потребителей. При выборочном распределении производитель вступает в соглашение с двумя или более розничными торговцами, которым предоставляется исключительное право продавать продукт компании в их районах. Этот метод распределения хорошо действует в больших городах или районах, где для хорошего обслуживания рынка необходимо более чем одно торговое предприятие и когда для получения существенной прибыли не требуется большого объема оборота. [4]

Выборочные распределения, связанные с нормальным распределением. Предположим, что последовательно и независимо производится п испытаний. [5]

Выборочные распределения, связанные с экспоненциальным распределением. Испытания на надежность могут быть организованы различными способами. Ограничимся только планами типа [ N, В, Т ], IN, В, г ] ( N, В, ( г, Т), IN, Б, Т ], ( N, Б, г ], [ N, Б, ( г, Т) ], IN, Б, 7U В начальный момент испытанию подвергаются N устройств. Предполагается, что наблюдения за отказами устройства производятся непрерывно, в результате чего отказы сразу же обнаруживаются. [6]

Выборочное распределение выборочной дисперсии - это одна из форм гамма-распределения, известная как хи-квадрат распределение, обозначаемое через х2 - Это распределение принимает разную форму для разного числа степеней свободы. [7]

Если выборочное распределение значительно отличается от нормального, то таблицы нормального распределения не дают удовлетворительного приближения для вероятности отклонения, превышающего фиксированное значение. [8]

Если выборочное распределение для г достаточно близко к нормальному, то это распределение можно использовать для проверки гипотезы о том, что р равно какому-либо заданному числу. Однако, если р значительно отличается от нуля, то выборочное распределение для г стремится к нормальному довольно медленно, и при п 46 следует ожидать, что получаемые с помощью стандартной ошибки результаты не очень точны. [9]

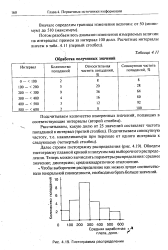Гистограмма распределения. [10]

Чтобы выборочное распределение как можно лучше соответствовало генеральной совокупности, необходимо брать больше значений. [11]

Если выборочное распределение не согласуется с законом нормального распределения, иногда удается получить хорошее аналитическое приближение при помощи Л - ряда Шарлье. [12]

Зная выборочное распределение статистики, мы можем рассматривать одни события как обычные, другие - как сравнительно редкие, третьи - как исключительные. [13]

Если выборочное распределение статистики имеет среднюю, равную соответствующему параметру генеральной совокупности, то говорят, что статистика является истинной оценкой параметра. [14]

Рассмотрим выборочное распределение средней величины. Такое распределение будет являться нормальным или приближаться к нему по мере увеличения объема выборки, независимо от того, имеет или нет нормальное распределение та генеральная совокупность, из которой взяты выборки. С увеличением числа выборок средняя для всех выборок будет приближаться к генеральной средней. [15]

Страницы: 1 2 3 4