Выборочное распределение

Cтраница 3

Часто бывает важно знать выборочные распределения экстремальных значений, v - x значений, широты и других подобных характеристик выборки. Сейчас мы рассмотрим некоторые свойства этих распределений. [31]

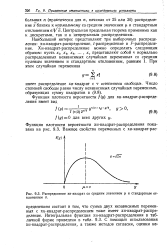Распределение хи-квадрат со средним значением ц и стандартным отклонением а. [32]

Наибольший интерес представляют три выборочных распределения: хи-квадрат-распределение, / - распределение и / - распределение. [33]

Выше мы отмечали, что выборочное распределение дисперсии следует, после соответствующего преобразования, х2 - РаспРе - делению. [34]

Стъю дента распределение) описывают выборочные распределения различных функций от нормально распределенных результатов наблюдений и используются для построения доверительных интервалов и статистич. [35]

Ряд других важных для приложений выборочных распределений и их характеристик будет указан в следующих параграфах. [36]

Распределения этих случайных величин называются выборочными распределениями. [37]

ЭМПИРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ, распределение выборки, выборочное распределение - распределение вероятностей, которое определяется по выборке для оценки истинного распределения. [38]

Располагая выборочными статистическими показателями и знаниями выборочных распределений этих показателей, мы готовы оценить параметры генеральной совокупности анализируемых данных. Однако может быть необходимым добиться некоторой степени смещенности с целью получения меньшей дисперсии. [39]

Теперь приступим к и мучен ню выборочных распределений, связанных с многомерной нормальной генеральной совокупностью. [40]

В следующем п 6.8 приводится ряд других важнейших выборочных распределений. Они лежат в основе построения доверительных интервалов для параметра т при неизвестной дисперсии з2, для дисперсии о2, а также играют большую роль и в теории статистической проверки гипотез. [41]

Кроме того, можно показать, что выборочное распределение х является в определенном приближении нормальным. Для данного распределения оценка дисперсии может быть получена следующим образом. [42]

Существенное значение для статистического анализа данных имеет выборочное распределение отношения двух дисперсий. [43]

Традиционно применяются три основных метода реализации: экстенсивное, исключительное и выборочное распределение изделий на рынке. [44]

Выборочное распределение. [45]

Страницы: 1 2 3 4