Гипергеометрическое распределение

Cтраница 1

Гипергеометрическое распределение используется в задачах контроля качества изделий. Оно дает распределение доли брака в выборке из контролируемой партии. [1]

Гипергеометрическое распределение характеризуется тремя параметрами: 1) р0 - может иметь любое значение между 0 и 1; 2) п - целое положительное число; 3) N п - целое положительное число. [2]

Гипергеометрическое распределение легко обобщить на случай, когда исходная генеральная совокупность объема п содержит несколько классов элементов. Например, пусть генеральная совокупность содержит три класса объемом п, п и п - i - n соответственно. [3]

Гипергеометрическое распределение имеет случайная величина Хт - число объектов, обладающих заданным свойством, среди п объектов, случайно извлеченных ( без возврата) из совокупности N объектов, М из которых обладают этим свойством. [4]

Гипергеометрическое распределение широко используется в практике статистического приемочного контроля качества промышленной продукции, в задачах, связанных с организацией выборочных обследований, и других областях. [5]

Гипергеометрическое распределение возникает следующим образом. Из нашего замечания и определения биномиальных коэффициентов следует, что / ( х А, J9, п) 0 при х А или п - х В. [6]

Гипергеометрическое распределение используется при решении задач контроля качества продукции. [7]

Гипергеометрическое распределение обладает свойствами, аналогичными свойствам биномиального распределения; оно также принадлежит к числу одномодальных распределений. [8]

Оцениваемым параметром гипергеометрического распределения является D; Nun считаются заданными величинами, а исходными данными для построения оценок для D будет выборочное значение d - число дефектных изделий среди выбранных п изделий. [9]

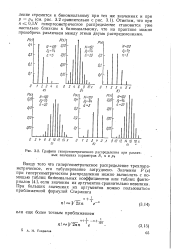Графики гипергеометрического распределения при различных значениях параметров N, п п ро. [10]

Ввиду того что гипергеометрическое распределение трехпара-метрическое, его табулирование затруднено. Значения Р ( х) при гипергеометрическом распределении можно вычислять с помощью таблиц биномиальных коэффициентов или таблиц факториалов [4], если значения их аргументов сравнительно невелики. [11]

При п0 Ш гипергеометрическое распределение близко к биномиальному. [12]

Геологические области применимости гипергеометрического распределения близки к тем, где привлекаются модели Бернулли. [13]

Прежде чем дать определение гипергеометрического распределения, рассмотрим задачу. Обозначим через X случайную величину - число т стандартных изделий среди п отобранных. [14]

Набор чисел (1.5) называют гипергеометрическим распределением. [15]

Страницы: 1 2 3 4