Гипергеометрическое распределение

Cтраница 2

Вычисляют их на основании свойств гипергеометрического распределения. [16]

Если случайная величина X распределена согласно гипергеометрическому распределению ( 1), то ( упр. [17]

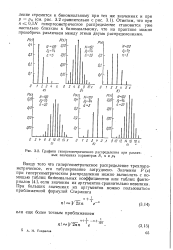Графики гипергеометрического распределения при различных значениях параметров N, п п ро. [18]

Отметим, что при ns OJN гипергеометрическое распределение становится уже настолько близким к биномиальному, что на практике можно пренебречь различием между этими двумя распределениями. [19]

Согласно американским и британским нормам BS1008 гипергеометрическое распределение заменяется биномиальным. [20]

В британских нормах BS600R и BS1313 гипергеометрическое распределение заменяется распределением Пуассона. Пуассона в качестве контрольной границы. [21]

Типичная схема, в которой появляется гипергеометрическое распределение, такова: проверяется партия готовой продукции, которая содержит Np годных и N ( - р) негодных объектов. Случайным образом выбирают п объектов. Число годных объектов среди выбранных и описывается гипергеометрическим распределением. [22]

Вероятность Р ( с) подчиняется гипергеометрическому распределению. Обычно для приближенного вычисления Р ( с) используется биномиальное или пуассоновское приближение. [23]

Эта модель приводит к так называемому гипергеометрическому распределению числа поездов. [24]

Набор вероятностей ( 7) называется гипергеометрическим распределением. Это распределение часто используется при решении некоторых задач. [25]

Близким по условиям возникновения к биномиальному распределению является гипергеометрическое распределение. [26]

В § 6 мы отмечали, что члены гипергеометрического распределения должны давать в сумме единицу. [27]

Убедиться в том, что распределение статистики Т ( гипергеометрическое распределение Я ( 9, N, п)) имеет монотонное отношение правдоподобия. [28]

Распределение вероятностей, соответствующее ( 1), называют гипергеометрическим распределением. [29]

Точная функция плотности вероятностей, описывающая дискретные распределения, является гипергеометрическим распределением, но обычно в качестве приближения используется биномиальное распределение. Если выборка мала по сравнению с генеральной совокупностью ( менее 20 %), это приближение является вполне удовлетворительным. [30]

Страницы: 1 2 3 4