Гипергеометрическое распределение
Cтраница 3
Совокупность чисел pk, заданную ( 5), называют гипергеометрическим распределением. [31]
Можно показать, что при N - оо функция вероятностей (4.14) гипергеометрического распределения стремится к соответствующей функции (4.1) биномиального закона. [32]
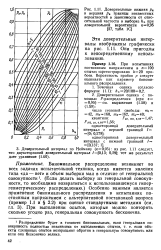 |
Доверительные нижняя ря и верхняя ря границы неизвестных вероятностей в зависимости от относительной частости в выборке Л при доверительной вероятности е0 95 [ 27, 1C ]. [33] |
Если делать выборку из генеральной совокупности, то необходимо возвратиться к использовавшемуся гипергеометрическому распределению. Особенно важным является применение биномиального распределения в испытаниях постоянным напряжением с альтернативной постановкой вопроса ( пример 1.1 и § 2.2) при оценке стандартными методами ( см. гл. При выполнении опытов, которые можно повторять сколько угодно раз, генеральная совокупность бесконечна. [34]
Основой правильной контрольной карты для доли брака или для числа бракованных деталей является гипергеометрическое распределение. Связанные с ним числовые расчеты затруднительны, поэтому гипергеометрическое распределение заменяется приближенным. [35]
Число Sk черных предметов, вошедших в выборку, является случайной величиной с гипергеометрическим распределением ( гл. [36]
Заметим, что если п значительно меньше N ( практически если п0 Ш), то гипергеометрическое распределение дает вероятности, близкие к вероятностям, найденным по биномиальному закону. [37]
 |
Совместное распределение ( Л, Хг в примере а. [38] |
Если выбор производился без возвращения, то вероятность Р А - ] А1, X2 k2 ] определяется двойным гипергеометрическим распределением (6.5) гл. II, а Х имеет обычное гипергеометрическое распределение (6.1) гл. [39]
Этот вопрос имеет четкий математический ответ, и сводится к хорошо известной проблеме комбинаторики, ведущей к так называемой гипергеометрическому распределению. [40]
При выборочном контроле всегда имеется и тот, и другой риск, величины которых можно вычислить точно, пользуясь гипергеометрическим распределением, и приближенно, пользуясь биномиальным распределением или распределением Пуассона в зависимости от действительной доли брака р в партии. [41]
Случайная величина d ( п), принимающая целочисленные значения от О до и с вероятностью, задаваемой формулой ( 1), имеет гипергеометрическое распределение. [42]
Случайную величину Хт, распределенную по биномиальному закону (4.1), можно интерпретировать как число т объектов, обладающих данным свойством, из общего числа п объектов, случайно извлеченных из некоторой воображаемой бесконечной совокупности, доля р объектов которой обладает этим свойством. Поэтому гипергеометрическое распределение можно рассматривать как модификацию биномиального распределения для случая конечной совокупности, состоящей из N объектов, М из которых обладают этим свойством. [43]
В теории последующих оценок важное место занимают оценки априорного распределения числа дефектных изделий в последовательности партий, поскольку эффективность использования плана контроля зависит от априорного распределения числа дефектных изделий. В основе априорного распределения - гипергеометрическое распределение, которое при наличии определенных условий заменяется биномиальным или пуассоновским распределением. [44]
Если выбор производился без возвращения, то вероятность Р А - ] А1, X2 k2 ] определяется двойным гипергеометрическим распределением (6.5) гл. II, а Х имеет обычное гипергеометрическое распределение (6.1) гл. [45]
Страницы: 1 2 3 4