Максвелл-больцмановское распределение
Cтраница 3
Обе эти теории основаны на главном предположении, что скорость элементарного процесса при наличии статистического равновесия ( максвелл-больцмановского распределения) и при его отсутствии одинакова. На основе этого предположения в простой теории столкновений для нахождения числа реагирующих молекул с заданными скоростями используется максвелловское распределение. [31]
Возвращаясь к общему рассмотрению метода активированного комплекса, следует отметить, что основное исходное положение - наличие равновесного Максвелл-Больцмановского распределения в ходе реакции не всегда справедливо. [32]
Возвращаясь к общему рассмотрению метода активированного комплекса, следует отметить, что основное исходное положение - наличие равновесного Максвелл-Больцмановского распределения в ходе реакции - - не всегда справедливо. [33]
В основе теории активированного комплекса лежит предположение о том, что распределение молекул по состояниям отвечает статистически равновесному максвелл-больцмановскому распределению, которое не нарушается существенно в ходе химической реакции. Это предположение несколько противоречиво: мы допускаем, что равновесное распределение энергии между исходными молекулами и активированными комплексами поддерживается в течение всего процесса, и в то же время считаем, что каждый активированный комплекс неизбежно превращается в продукты реакции. [34]
Между процессами переноса вещества и тепла имеется глубокая аналогия: для систем с достаточно большим числом частиц и установившимся максвелл-больцмановским распределением уравнения диффузии и теплопередачи имеют один и тот же вид, а соответствующие параметры не отличаются по порядку величины. [35]
Для химически инертного растворителя это можно было ожидать, если считать, что роль молекул растворителя сводится к поддержанию максвелл-больцмановского распределения и, следовательно, термически равновесной концентрации активных молекул. Однако в некоторых других растворителях ( азотной кислоте, дихлорпропане) полупятиокись азота разлагается приблизительно в 25 раз медленнее, энергия активации увеличивается примерно до 28300 кал / моль. [36]
Для реакций, скорость протекания которых можно измерить обычными методами, возможен следующий критерий согласованности числа активных частиц в реагирующей системе с максвелл-больцмановским распределением. Если энергия активации достаточно велика, то число активных частиц составит незначительную долю всех частиц системы. Незначительная их убыль в ходе реакции будет легко восполняться в результате активации при столкновениях. Если же энергия активации мала, то значительная доля частиц является реакционноспособ-ной, и максвелл-больцмановское распределение уже не будет успевать восстанавливаться за счет столкновений. [37]
Для реакций, скорость протекания которых можно измерить обычными методами, возможен следующий критерий согласованности числа активных частиц в реагирующей системе с максвелл-больцмановским распределением. Если энергия активации достаточно велика, то число активных частиц составит незначительную долю всех частиц системы. Незначительная их убыль в ходе реакции будет легко восполняться в результате активации при столкновениях. Если же энергия активации мала, то значительная доля частиц является реакционноспособной, и максвелл-больцмановское распределение уже не будет успевать восстанавливаться за счет столкновений. [38]
Макроскопическое выражение производства энтропии накладывает ограничивающее условие на химические реакции, которое обычно выполняется: при химической реакции не должно происходить существенного нарушения максвелл-больцмановского распределения для каждого из участвующих компонентов. [39]
Неравенство ( IV, 17) показывает, что при данной энергии активации любой процесс с повышением температуры может перейти в область несоблюдения максвелл-больцмановского распределения. [40]
В основе метода переходного состояния лежит предположение, что протекание реакции не нарушает существенно распределения молекул по состояниям, так что оно отвечает статистически равновесному Максвелл-Больцмановскому распределению. Область применимости этого предположения совпадает с областью применимости закона действующих масс и уравнения Аррениуса. [41]
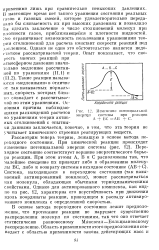 |
Изменение потенциальной. [42] |
В основе метода переходного состояния лежит предположение, что протекание реакции не нарушает существенно распределения молекул по состояниям, так что оно отвечает статистически равновесному Максвелл-Больцмановскому распределению. [43]
Как говорилось выше, в подобных случаях ( когда энергетические уровни перекрывают большой диапазон энергий), можно получить различные значения температуры вследствие отклонений энергий возбуждающих частиц от максвелл-больцмановского распределения. Если предположить далее, что основными процессами возбуждения в плазменной струе являются соударения с электронами, и учесть, что эффективность ударных процессов растет пропорционально концентрации электронов, то можно объяснить расхождение в измеренных значениях температуры недостаточной концентрацией электронов, которая не превышает 101в см-3. Таким образом, указанные авторы пришли к выводу, что дуги в инертных газах и водороде не являются равновесными системами при малых концентрациях электронов. [44]
Далее, более детального рассмотрения ( чем это было сделано до настоящего времени) требуют: теория мономолекулярных реакций, особенно вопрос об активации и дезактивации молекул при столкновениях, и вопрос о сохранении максвелл-больцмановского распределения энергии в реагирующем газе. [45]
Страницы: 1 2 3 4