Радиальное распределение - электронная плотность
Cтраница 1
Радиальное распределение электронной плотности и температуры, измеренное на Стеллараторе WIIB методом лазерного рассеяния; О - результаты микроволновых измерений. [1]
Сравним теперь радиальное распределение электронной плотности на 3s -, Зр - и Зй-орбиталях. Хотя d - орбиталь меньше ( наиболее вероятные радиусы убывают в порядке 3s Зр 3d), наличие одного узла и внутриузлового максимума в Зр-орбитали и двух узлов и двух внутриузловых максимумов в Ss-орбитали вызывает большее влияние ядра на них. Следовательно, энергии этих орбиталей изменяются в следующем порядке: 3d Зр 3s, что и было сформулировано выше в принципе минимума энергии. [2]
Расчет радиального распределения электронной плотности ( анализ Фурье) и расчет по методу наименьших квадратов были выполнены на счетной машине IBM 7090 по разработанным нами и Гантцелем и др. [4] программам. [3]
Кривые радиального распределения электронной плотности для таких катализаторов содержат межатомные расстояния, характерные для г.ц. к, структуры металла, и измененные по площади межатомные расстояния структуры шпинели. [4]
Исследование радиального распределения электронной плотности углеродных атомов методом дифракции рентгеновских лучей показывает, что возникающие на диаграммах пики соответствуют тригональным углерод-углеродным связям длиной 0 142 нм, отражающим существование гексагональных углеродных слоев, и тетраэдрическим связям длиной 0 155 нм. Возможно, что длина последних связей определяется деформацией гексагональных плоскостей, соответственно изменяющей межатомные расстояния, поэтому указанные связи можно называть нетривиальными. [5]
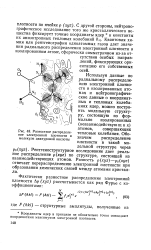 |
Разностное распределение электронной плотности в молекуле циануровой кислоты. [6] |
Используя данные по радиальному распределению электронной плотности в изолированных атомах и нейтронографиче-ские данные о координатных и тепловых колебаниях ядер, можно построить модельную структуру, состоящую из формально изолированных ( невзаимодействующ и х) атомов, совершающих тепловые колебания. [7]
 |
Разностное распределение электронной плотности в молекуле циануровой кислоты. [8] |
Используя данные по радиальному распределению электронной плотности в изолированных атомах и нейтронографиче-ские данные о координатных и тепловых колебаниях ядер, можно построить модельную структуру, состоящую из формально изолированных ( невзаимодействую щ и х) атомов, совершающих тепловые колебания. [9]
На рис. 33.11 изображены радиальные распределения электронной плотности и температуры, измеренные в типичном режиме при ijj 0 2д на Стеллараторе WIIB методом лазерного рассеяния. [10]
 |
Радиальное распределение вероятности нахождения электрона ( электронной плотности на расстоянии г от ядра. [11] |
На рис. 9 показано радиальное распределение электронной плотности для s -, р - и d - орбиталей атома водорода. Как видно из рисунка, число максимумов на кривой распределения электронной плотности определяется главным квантовым числом. Для s - электронов число максимумов равно значению главного квантового числа, для р-электронов - на единицу меньше, а для d - электронов - на две единицы меньше значения главного квантового числа. [12]
Множитель Rni ( г) г3 определяет радиальное распределение электронной плотности - вероятность найти электрон на определ. [13]
Это уравнение в отличие от (3.14) определяет радиальное распределение межмолекулярной электронной плотности. [14]
Для объяснения строения жидкостей часто используются кривые радиального распределения электронной плотности, получаемые методом рент-геноструктурного анализа. [15]
Страницы: 1 2 3 4 5