Радиальное распределение - электронная плотность
Cтраница 4
На рис. 3.4 дано сравнение функции Р ( г) ( п 3, / 1), вычисленной из уравнений Хартри и Хартри-Фока. Легко заметить, что метод Хартри ведет к недостаточно точному радиальному распределению электронной плотности для валентных электронов. [46]
В случае веществ с неупорядоченной структурой можно говорить лишь о вероятности расположения центров атомов друг относительно друга. Если в качестве мельчайшей структурной единицы взять электрон, то получается аналогичная функция радиального распределения электронной плотности Ц ( г) 471 г р ( г), где О ( Г) - число электронов на единицу объема. Поскольку начало отсчета выбирается на том или ином атоме ( или электроне) произвольно, то функции р ( Л) и U. [47]
 |
К вычислению атомного фактора. [48] |
Очевидно, что в сферическом слое толщиной dr на расстоянии г находится 4 лг2 p ( r) drU ( r) dr электронов. Функция U ( r) 4 лг2 р ( г) называется функцией радиального распределения электронной плотности. [49]
За последнее время для изучения фазового состава находит применение метод рентгеноструктурного анализа путем определения электронной плотности стекловидных веществ. Так, при исследовании фосфатных стекол с различным молярным отношением СаО / Р205 Ван-Везером [7] были получены кривые радиального распределения электронной плотности. Расшифровка этих кривых путем измерения плош адей под пиками показала характер связи между электронами ( Р, О, Са): так, 4 2 атома кислорода расположены вокруг одного атома фосфора, а каждый атом кальция окружен 6 - 8 - ю атомами кислорода. [50]
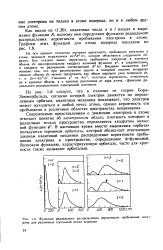 |
Функции радиального распределения вероятности пребывания электрона для различных состояний атома водорода. [51] |
На оси ординат отложены значения вероятности пребывания электрона в атоме, заданные выражением 4лг2Л2 ( г), которое объясняется следующим образом. Умножив у2 на 4ЛГ2, получаем вероятность, отнесенную не к единице объема, а к единице расстояния от ядра атома, - функцию радиального распределения электронной плотности. [52]
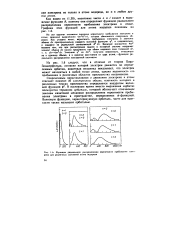 |
Функции радиального распределения вероятности пребывания элею-рона для различных состояний атома водорода. [53] |
На оси ординат отложены значения вероятности пребывания электрона в атоме, заданные выражением 4лг2Л2 ( г), которое объясняется следующим образом. Умножив V2 на лг2, получаем вероятность, отнесенную не к единице объема, а к единице расстояния от ядра атома, - функцию радиального распределения электронной плотности. [54]
Расплав обычно имеет меньшую плотность, чем соответствующий кристалл, и поэтому более низкое КЧ. В этой таблице для кристаллов приведены кратчайшие межатомные расстояния и КЧ, для расплавов-среднее статистическое число ближайших соседей и соответствующие им длины связей, полученные методом радиального распределения электронной плотности. [55]
Оба метода дают согласующиеся результаты, в снова в качестве примера на рис. 32 9 приведены профили пе, снятые на двух установках. Радиальное распределение электронной плотности, как правило, хорошо аппроксимируется квадратичной параболой. [56]
Исходным пунктом одноэлектронного приближения для атомов с большим числом электронов также является уравнение Шредин-тера (1.21) с гамильтонианом (1.20) с тем, однако, отличием, что кулоновский потенциал - - Zelr заменяется другим сферически-симметричным потенциалом U ( г), в котором наряду с действием заряда ядра учтено экранирование его остальными электронами. ЭФФ е / г гДе эфф означает эффективный заряд ядра, экранированного внутренними электронами. Так как радиальное распределение электронной плотности, определяемое функцией Rni ( г), зависит от квантового числа I, экранирующее действие для электронов с различными I оказывается разным, поэтому энергия стационарного состояния зависит теперь от обоих квантовых чисел п и I. Отметим, что в то время как радиальная составляющая волновой функции изменяется из-за экранирования, угловая компонента остается такой же, как у атома водорода. [57]
В качестве иллюстрации можно привести пары элементов, различие в свойствах которых общеизвестно и может быть объяснено с точки зрения представления о кайносимметричных орбиталях. Эти особенности кайносимметричных элементов обусловлены меньшим экранированием валентных электронов. Внутренние максимумы радиального распределения электронной плотности для некаиносимметричных валентных орбиталей совпадают с аналогичными максимумами заполненных внутренних орбиталей той же симметрии. Вследствие этого некай-носимметричные электроны испытывают значительно больший эффект экранирования, из-за чего их связь с ядром существенно слабее по сравнению с кайносимметричными электронами. [58]
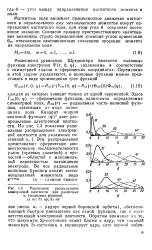 |
Радиальное распределение. [59] |
Здесь Yim ( Q, ф) - сферические функции, однозначно определяемые симметрией поля, Rmi ( r) - радиальная часть волновой функции, зависящая от вида потенциала поля. Квадрат модуля волновой функции х ( з 2 дает распределение электронной плотности. На рис. 1.3 показаны радиальные распределения электронной плотности для различных состояний п, I. [60]
Страницы: 1 2 3 4 5