Радиальное распределение - электронная плотность
Cтраница 2
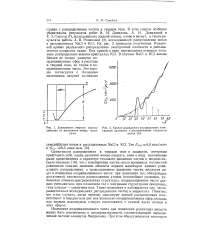 |
Зависимость энергии взаимо - [ IMAGE ] Кривая радиального распределения элек-действия от расстояния между части - тронной плотности в расплавленном хлористом цами. калии. [16] |
На рис. 2 приведена полученная Романовой кривая радиального распределения электронной плотности в расплавленном хлористом калии. В случаях Nad и КС1 весьма близки не только радиусы координационных сфер в расплаве и твердой соли, но также и координационные числа. [17]
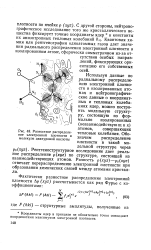 |
Разностное распределение электронной плотности в молекуле циануровой кислоты. [18] |
Квантовая химия или рентгенография одноатомных газов дает значения радиального распределения электронной плотности в изолированном атоме, сферически симметричном из-за отсутствия особых направлений, фиксирующих ориентацию его собственных осей. [19]
 |
Форма р-орбиталей. [20] |
На рис. ЗЛО, б приведены для сравнения функции радиального распределения электронной плотности для Is -, 2s - и Ss-орбитали. С увеличением функции вероятности образуют несколько концентрических областей ( для ls - орбитали - одну, для 2s - две и для 3s - три), вероятность пребывания электрона между которыми равна нулю. Орбиталь ( п1) везде положительна, а s - орбитали с более высокими квантовыми числами п имеют чередующиеся положительные и отрицательные области. [21]
Недавно в работе японских исследователей [188] Agl было изучено методом радиального распределения электронной плотности, т.е. типично жидкостным методом рентгеноструктурного анализа. Вследствие хаотичного распределения катионов Ag на рентгенограмме проявляется гало, анализ которого позволил определить КЧд85 и rAg Ag 2 75 А. [22]
Определение ближнего порядка расположения атомов в стеклообразных метафосфатах при помощи радиальных распределений электронной плотности [1,2] хотя и указывает на сохранение полифосфатных цепочек, однако не дает возможности определить, насколько упорядоченным является взаимное расположение цепочек. При параллельном расположении в стекле возможно сохранение некоторых элементов кристаллической структуры соответствующего полифосфата, в частности некоторых атомных плоскостей, параллельных осям цепочек. С целью выяснения этого вопроса нами было проведено рентгенографическое исследование стеклообразных метафосфатов калия, кальция, магния, марганца и цинка. [23]
В отличие от перечисленных все остальные орбитали той же симметрии имеют дополнительные максимумы на кривых радиального распределения электронной плотности. Таким образом, для кайносимметричных орбиталей характерно отсутствие внутренних заполненных орбиталей той же симметрии. [24]
В отличие от перечисленных все остальные орбитали той же симметрии имеют дополнительные максимумы на кривых радиального распределения электронной плотности. Таким образом, для кайносимметричных орбиталей характерно отсутствие внутренних заполненных орбиталей той же симметрии. Это приводит к усилению связи кайносимметричных электронов с ядром за счет существенного ослабления эффекта экранирования, уменьшению орбитальных атомных радиусов, повышению потенциалов ионизации, а следовательно, к ослаблению металлических свойств кайносимметричных элементов по сравнению с некайно-симметричными. [25]
Можно видеть, что положение максимумов на этой кривой почти такое же, как и на кривой радиального распределения электронной плотности ( см. рис. 3.2), а именно при К. [26]
 |
Суммарная вероятность нахождения электронов в атомах Н, Li, В, Ne внутри сферического слоя радиусом г и орбитальные радиусы атомов соответствующих элементов ( указаны цифрами. [27] |
В то же время квантовая механика позволяет произвести расчет вероятности нахождения электрона внутри сферического слоя радиусом г, построить схематические кривые радиального распределения электронной плотности, получить фигуры с поверхностью, ограничивающей, например, 95 % плотности распределения электронов. Радиусы главных максимумов радиальной плотности электронов отдельных орбиталей атомов н ионов называются их орбитальными радиусами. Орбитальный радиус ни в коей мере не определяет границ распространения электронов рассматриваемой орбитали, а лишь максимум их электронной плотности. [28]
 |
Радиальное распределение вероятности пребывания электрона для различных состояний атома водорода. [29] |
Умножив ф2 на 4лг2, получаем вероятность, отнесенную не к единице объема, а к единице расстояния от ядра атома - функцию радиального распределения электронной плотности. [30]
Страницы: 1 2 3 4 5