Радиальное распределение - электронная плотность
Cтраница 3
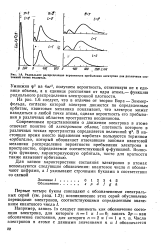 |
Радиальное распределение вероятности пребывания электрона для различных состояний атома водорода. [31] |
Умножив ф2 на 4яг2, получаем вероятность, отнесенную не к единице объема, а к единице расстояния от ядра атома - функцию радиального распределения электронной плотности. [32]
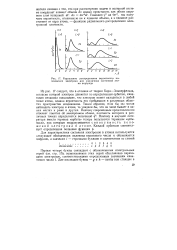 |
Радиальное распределение вероятности на. [33] |
Умножив ф2 на 4irr2, мы получаем вероятность, отнесенную не к единице объема, а к единице расстояния от ядра атома, - функцию радиального распределения электронной плотности. [34]
Проведено рентгенографическое исследование стеклообразных мстафосфатов калия, магния, кальция, марганца и цинка. Радиальные распределения электронной плотности соответствуют тому, что каждый атом фосфора тетраэдрически окружен четырьмя атомами кислорода и каждый тетраэдр двумя вершинами связан с двумя соседними тетраэдрами. Анализ периодичностей, содержащихся в кривых интенсивности рассеяния рентгеновских лучей, свидетельствует о сохранении параллельного расположения полифосфатных цепочек в стеклообразном мотафосфате калия. Упорядоченность структур других исследованных метафосфатов является следствием жесткости катионных полиэдров. [35]
Эти особенности кайносимметричных элементов обусловлены меньшим экранированием валентных электронов. Внутренние максимумы радиального распределения электронной плотности для некайносимметричных валентных орбиталей совпадают с аналогичными максимумами заполненных внутренних орбиталей той же симметрии. Вследствие этого некайносимметричные электроны испытывают значительно больший эффект экранирования, из-за чего их связь с ядром существенно слабее по сравнению с кайносимметричными электронами. [36]
Эти особенности кайносимметричных элементов обусловлены меньшим экранированием валентных электронов. Внутренние максимумы радиального распределения электронной плотности для некайносимметричных валентных орбиталей совпадают с аналогичными максимумами заполненных внутренних орбиталей той же симметрии. Вследствие этого некайносимметричные электроны испытывают значительно больший эффект экранирования, из-за чего их связь с ядром существенно слабее по сравнению, с кайносимметричными электронами. [37]
Главное квантовое число п характеризует общий запас энергии электрона. Оно зависит от среднего радиального распределения электронной плотности около ядра. [38]
На рис. 8 показано радиальное распределение электронной плотности для s -, р - и d - орбиталей атома водорода. Как видно из рисунка, число максимумов на кривой распределения электронной плотности определяется главным квантовым числом. [39]
Постановка задачи довольно проста. С другой стороны, используя данные по радиальному распределению электронной плотности в изолированных атомах и нейт-ронографические данные о координатных и тепловых колебаниях ядер, можно построить модельную структуру, состоящую из формально изолированных ( невзаимодействующих) атомов, совершающих тепловые колебания. Разность p ( xyz) - p0 ( xyz) отвечает перераспределению электронной плотности при образовании химических связей между атомами кристалла. Обычно такое разностное распределение называют деформационной электронной плотностью. [40]
Постановка задачи довольно проста. С другой стороны, используя данные по радиальному распределению электронной плотности в изолированных атомах и нейт-ронографические данные о координатных и тепловых колебаниях ядер, можно построить модельную структуру, состоящую из формально изолированных ( невзаимодействующих) атомов, совершающих тепловые колебания. Разность p ( xyz) - po ( xyz) отвечает перераспределению электронной плотности при образовании химических связей между атомами кристалла. Обычно такое разностное распределение называют деформационной электронной плотностью. [41]
На рис. 3.4 дано сравнение функции Р ( г) ( п 3, / 1), вычисленной из уравнений Хартри и Хартри-Фока. Легко заметить, что метод Хартри ведет к недостаточно точному радиальному распределению электронной плотности для валентных электронов. [43]
На рис. 10 дано сравнение функции Р ( г) ( п 3, / 1), вычисленной из уравнений Хартри и Хартри - Фока. Легко заметить, что метод Хартри ведет к недостаточно точному радиальному распределению электронной плотности для валентных электронов. [44]
Страницы: 1 2 3 4 5

