Нормальное распределение - случайная величина
Cтраница 1
Нормальное распределение случайной величины характеризуется совершенно определенными нормами разбросов исходов результатов испытаний по отношению к математическому ожиданию. [1]
При нормальном распределении случайной величины Нс максимум функции ( 14) будет в случае, когда левый и правый пределы будут расположены симметрично относительно МНС. [2]
При нормальном распределении случайных величин метод наименьших квадратов обосновывается в теории вероятностей как частный случай принципа максимума правдоподобия. [3]
Гри нормальном распределении случайных величин метод наименьших квадратов обосновывается в теории вероятностей как частлый случай-принципа максимума правдоподобия. [4]
Так как нормальное распределение случайной величины в виде (5.28) вполне определяется ее основным отклонением, то для оценки параметров на основании статистик достаточно знать основные ошибки этих статистик. [5]
Отсюда следует нормальное распределение случайной величины г) е параметрами Мд аа - f р и от, ао. Если а 0, то, согласно ( 10), в правой части выражения для / т ( г /) появится знак минус. [6]
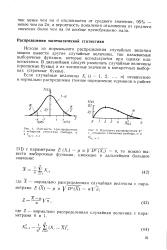 |
Плотность / - распределения с четырьмя степенями свободы, а.| Плотность распределения % 2 с четырьмя степенями свободы, гх и. [7] |
Исходя из нормального распределения случайных величин можно вывести другие случайные величины, так называемые выборочные функции, которые используются при оценке или испытании. [8]
 |
Отклонения размеров. [9] |
Кроме закона нормального распределения случайных величин, существуют другие математические законы распределения случайных величин, но они на производстве имеют меньшее применение. [10]
Характерными особенностями закона нормального распределения случайных величин является то, что центром распределения случайных величин является их среднее значение, что появление случайных величин с одинаковыми отклонениями от среднего, но с разными знаками ( в - f - и в -), равновероятно. Чем меньше и чем больше значение случайных величин, тем реже они встречаются. [11]
На основе закона нормального распределения случайных величин можно многократным измерением одних и тех же величин одним и тем же измерительным средством уменьшить влияние случайных ошибок, так как они осредняются и в итоге повышается точность результата измерения. [12]
На основе закона нормального распределения случайных величин можно многократным измерением одних и тех же величин одним и тем же измерительным средством уменьшить влияние случайных ошибок, так ка Они осредняются и в итоге повышается точность результата измерения. [13]
Характерными особенностями закона нормального распределения случайных величин является то, что центром распределения случайных величин является их среднее значение, что появление случайных величин с одинаковыми отклонениями от среднего, но с разными знаками ( в и в -), равновероятно. Чем меньше и чем больше значение случайных величин, тем реже они встречаются. [14]
 |
Кривые Ф ( X нормального распределения при трех значениях. [15] |
Страницы: 1 2 3 4