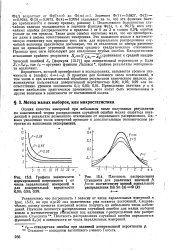
Нормальное распределение - случайная величина
Cтраница 3
В силу симметрии то же самое будет, если три средних квадр этических отклонения отложить влево, таким образом, для нормального распределения случайной величины практически все ее значения в генеральной совокупности ( с точностью до долей процента) укладываются на участке М [ Х ] За. Это позволяет, зная среднее квадр этическое отклонение и математическое ожидание случайной величины, ориентировочно указать интервал ее практически возможных значений. [31]
В таких случаях для определения параметров распределения более удобно пользоваться интегральными кривыми распределения, построенными на вероятностной сетке, так как кривая нормального распределения случайной величины на вероятностной сетке представляет собой прямую линию. [32]
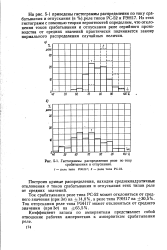 |
Гистограммы распределения реле по току срабатывания и отпускания. [33] |
Из этих гистограмм с помощью теории вероятностей определяем, что отклонения токов срабатывания и отпускания реле серийного производства от средних значений практически подчиняется закону нормального распределения случайных величин. [34]
Многочисленными измерениями деталей, обработанных по разным технологическим процессам ( на станках, автоматах, полуавтоматах и др.) установлено, что при обработке деталей распределение размеров соответствует широко известному закону нормального распределения случайных величин. [35]
По таблице значений вероятности ( см. табл. 1.2) отмечаем, что при X 1 81 вероятность Р ( X) очень мала ( менее 0 001), поэтому гипотеза о нормальном распределении случайной величины должна быть отвергнута. [36]
По таблице значений вероятности ( см. табл. 1.2) отмечаем, что при X 1 81 вероятность Я ( X) очень мала ( менее 0 001), поэтому гипотеза о нормальном распределении случайной величины должна быть отвергнута. [37]
 |
Зависимость приведенных ( /, энергетических ( / / и капитальных ( III затрат от номера варианта схемы, соответствующего возрастанию приведенных затрат. [38] |
Отметим еще, что возможные варианты технологических схем тазор аз деления являются вероятностными, случайными величинами по отношению к приведенным затратам на разделение, и функции распределения различных вариантов схем по приведенным затратам имеют характерный вид кривых нормального распределения случайных величин. [39]
При нормальном распределении случайных величин они хорошо поддаются анализу с помощью основных положений теории вероятности и математической статистики. [40]
Такая доля ошибок настолько мала, что ею пренебрегают даже в весьма ответственных измерениях. Это положение вошло в математическую статистику как правило трех сигм: для нормального распределения случайной величины практически достоверно, что ее отклонение от центра рассеивания не превзойдет утроенной величины среднего квадратического отклонения. Правило трех сигм используют для исключения грубых ошибок. [42]
Для оценки точности результата измерений необходимо знать две характеристики: среднюю квадратичную погрешность А5П и надежность а - вероятность попадания истинного значения измеряемой ьеличины в определенный доверительный интервал. Границы доверительного интервала обычно определяются через дисперсию, которая является параметром закона нормального распределения случайных величин. [43]
Заметим, что приведенное выше доказательство проводилось в рамках корреляционной теории без предположения о нормальном распределении случайных величин. [44]
Рассмотрим сначала случай скалярной функции скалярной случайной величины X. Если удастся подобрать прямую, достаточно близкую к кривой в области практически возможных значений случайной величины X ( в случае нормального распределения случайной величины X в интервале ( тх - Зох, тх - - Зах)), то можно рассчитывать на то, что математическое ожидание и дисперсия соответствующей линейной функции случайной величины X будут близкими к математическому ожиданию и дисперсии нелинейной функции. [45]
Страницы: 1 2 3 4