Дифракционное распределение

Cтраница 1

Дифракционное распределение (1.27), являющееся функцией угла г з, также можно преобразовать в функцию линейного расстояния в фокальной плоскости камерного объектива. [1]

Поскольку дифракционное распределение интенсивности от отверстий имеет вид, аналогичный дифракционному распределению от провода или щели, описанные приборы могут использоваться для контроля их диаметра и формы. Однако освещенность дифракционных максимумов при этом будет значительно ниже. Для увеличения их освещенности целесообразно увеличивать с помощью оптики плотность лазерного излучения в области отверстия, а также использовать более мощные лазеры. Кроме того, возникает необходимость обеспечения линейного сканирования дифракционных колец через их центр, для чего используют вместо щелевой диафрагмы перед фотоприемником точечную диафрагму либо видикон. [2]

Для получения полной картины учтем теперь дифракционное распределение, даваемое отдельной щелью решетки, состоящей из N щелей. [3]

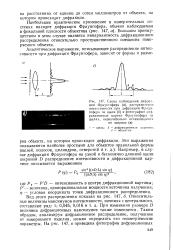
Дифракционные явления.| Эффекты дифракции в области тени. Экспонирование позитивного фоторезиста ФП-383 с применением цветного фотошаблона. Время экспонирования. / - 4. 2 - 6. 3 - 8. 4 - 14. [4]

Из практики фотолитографии известно различное проявление дифракционного распределения света за границей геометрической тени. [5]

Выходящий из диспергирующей системы пучок с дифракционным распределением попадает в камерный объектив, который образует в своей фокальной плоскости в направлении дисперсии пространственную дифракционную картину. [6]

Формулы (10.38) и (10.39) и определяют картину дифракционного распределения энергии по меридиональному и сагиттальному направлениям в кружке рассеяния для зрачка эллиптической формы. [7]

Схема наблюдения дифракции Фраунгофера ( а, распределение интенсивности при дифракции Фраунгофера па щели ( б и фотография дифракционных картин Фраунгофера на щелях, незначительно отличающихся по ширине ( в. [8]

Большим преимуществом в этом случае является инвариантность дифракционного распределения относительно пространственного смещения измеряемого объекта. [9]

Пространственная структура пучка в отсутствие турбулентности характеризуется дифракционным распределением интенсивности в поперечном сечении. [10]

Оптическая схема интерферометра ИТР-1. [11]

Сомножитель, зависящий от ширины щелей s, определяет дифракционное распределение света, а сомножитель, зависящий от расстояния между щелями ( лучами), определяет интерференционный эффект. [12]

Наибольший практический интерес представляют устройства, использующие предварительное преобразование дифракционного распределения в электрический сигнал с последующим его автоматическим анализом и выделением информации о расстоянии между экстремальными точками дифракционного распределения. Такие устройства позволяют повысить точность, быстродействие и автоматизировать процесс измерения. Следует заметить, что из-за многоступенчатого преобразования сигнала в таких устройствах не всегда удается с достаточной точностью расчетным путем связать абсолютное значение измеряемого размера с показаниями оконечного регистрирующего прибора и такие измерители, как правило, нуждаются в предварительной калибровке. В измерителях этого типа чаще всего осуществляют измерение временного интервала, соответствующего расстоянию между выбранными экстремальными точками электрического сигнала, описывающего дифракционное распределение. Ниже приводится описание наиболее перспективных измерительных устройств. [13]

Схемы видов пространственного фильтра из щелевых апертур ( а и муаровой картины, образующейся при пропускании дифракционной картины через фильтр ( б. [14]

В них используется однозначная зависимость координат точек минимальной интенсивности дифракционного распределения от размера изделия. Положение всех этих точек может быть найдено с помощью фильтра, состоящего из ряда прозрачных щелевых апертур, расположенных по отношению к дифракционному распределению так, что прошедшая интенсивность равна нулю. [15]

Страницы: 1 2 3 4