Классическое распределение

Cтраница 1

Распределение частиц газа по ктронов твердом теле объеди.| Схема энергетических зон для электронов в проводниках ( а, б, полупроводниках ( а и изоляторах ( г. [1]

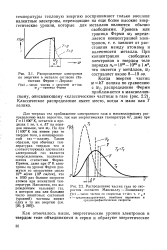
Классическое распределение наблюдается, когда п мало или Т велико. [2]

Классические распределения (7.18), (7.19) и (7.20) имеют ограниченную применимость. Критерий, устанавливающий, в каких пределах законно использование классической статистической физики, будет дан в § 21.4.) В этом они уступают строгим квантовым соотношениям. Однако вычисления по квантовым формулам часто оказываются слишком сложными. Поэтому в конкретных расчетах часто применяются приближенные квазиклассические выражения. [3]

Распределение электронов по энергиям в металле согласно статистике Ферми - Дирака. F ( w - число частиц с энергией ш Дш.| Распределение частиц газа по скоростям согласно Максвеллу - Больцману. F ( v - число частиц со скоростью v Av. v, v и v - среднеквадратичная, наиболее вероятная н среднеарифметическая скорости. [4]

Классическое распределение имеет место, когда п мало или Т велико. [5]

Допущение о классическом распределении энергии реагирующих частиц [172] является приемлемым для туннельного перехода протона в реакциях, протекающих, например, в газовой фазе. Однако в случае квазикристаллической среды, такой, например, как жидкая вода ( или лед), перенос протона от Н3О должен рассматриваться как происходящий из дискретных квантовых состояний, а не из непрерывного ряда состояний. [6]

Эти формулы заменяют классическое распределение Максвелла. [7]

Ширина распределения импульсов ультрахолодных атомов натрия, находящихся в поле пространственно модулированной стоячей лазерной волны, как функция параметра модуляции Л. Сплошные тонкие линии построены с помощью стандартного отображения и. Сплошная и штриховая жирные линии демонстрируют результаты двух различных квантовомеханических расчетов, а штрих-пунктирная линия - результат классического моделирования. При А 2 наблюдается проявление динамической локализации. [8]

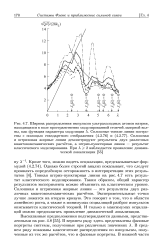
В среднем ряду показаны классические распределения по импульсам, полученные из тех же расчетов, что и фазовые портреты. [9]

Распределение (21.8) является квантовым аналогом классического распределения Максвелла - Больцмана (17.1) и, по сути дела, совпадает с ним. [10]

Закон, строго вытекает из классического распределения Больцмана стиц идеального газа при описании движения молекул уравнениями) й механики. Кроме того, оказывается, что классическая статистика Больцмана является лишь приближением, которое выполняется не для всякого идеального газа. Например, к электронному газу в металле даже при обычных условиях статистика Больцмана неприменима ( см. гл. [11]

В задачах 2.10 - 2.28 изучаются некоторые известные классические распределения дискретного и непрерывного типа. [12]

Распределение электронной плотности в молекуле Н2. [13]

Электронное облако симметрично обтекает оба ядра, демонстрируя классическое распределение заряда при ковалентнои связи. [14]

Диагональные матрицы р ] Cjwjb) 0 l соответствуют классическим распределениям вероятностей на множестве базисных векторов. [15]

Страницы: 1 2 3 4