Больцмановское распределение

Cтраница 1

Больцмановское распределение применимо только к системам, находящимся в термическом равновесии. [1]

Применяя больцмановское распределение, получаем выражение для f ( vi, Z), где Z - координата вдоль поля. Для координат х и у сохраняется простое одномерное максвелловское распределение. При этом не учитывается изменение скорости при ионизации. [2]

Нарушение больцмановского распределения приводит к тому, что константа скорости / гд, определяемая из условия равновесия (19.19), оказывается на порядок больше ее значения в начальной стадии реакции. [3]

Вследствие больцмановского распределения населенно-стей уровней мод инверсная населенность одновременно образуется и на большом числе переходов, соответствующих полосам секвенции и горячим полосам. Усиление на этих переходах значительно меньше, и для получения генерации на них в резонатор лазера вносят частотно-селективные потери, посредством к-рых подавляется гене-раиия на более сильных переходах. [4]

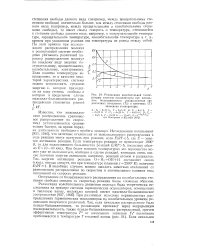Релаксация колебательной температуры системы осцилляторов при начальном больцмановском распределении при различных начальных ( То и конечных ( Т значениях температуры. [5]

Отступление от больцмановского распределения по колебательным степеням свободы связано со скоростью реакции более сложным образом. [6]

Приведенные примеры больцмановского распределения ччгтии в силовых внешних полях свидетельствуют о большой практической значимости полученных соотношений. [7]

Это соответствует обычному больцмановскому распределению дырок в задерживающем поле. [8]

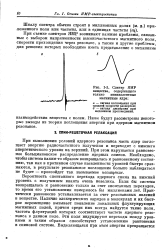Спектр ЯМР. [9]

При этом нарушается равновесное больцмановское распределение ядерных спинов. Необходимо, чтобы система каким-то образом возвращалась к равновесному состоянию, так как в противном случае населенности уровней быстро сравняются, в результате резонансное поглощение больше наблюдаться не будет - произойдет так называемое насыщение. [10]

Если обратиться к больцмановскому распределению ядер ных спинов ( см. разд. I), то очевидно, что с ростом на пряженности магнитного поля будет происходить рост населен ности состояния с низкой энергией. Например, отношение сигнал / шум, измеренное п квартету метиленовых протонов этилбензола ( рис. III. [11]

Разброс энергии обусловлен больцмановским распределением скоростей, которое и определяет нижний предел, равный 0 1 эв при температуре 103 К. [12]

При тепловом равновесии устанавливается больцмановское распределение числа частиц по этим двум энергетическим уровням, причем на нижнем уровне находится большее число частиц. [13]

Это выражение фактически является квантовым больцмановским распределением К ( Е) 8Е, дающим равновесную долю молекул в заданном интервале энергии. [14]

Кривые на первых диаграммах представляют собой больцмановское распределение. [15]

Страницы: 1 2 3 4