Большая Энциклопедия Нефти и Газа

Никогда не называй человека дураком. Лучше займи у него в долг. Законы Мерфи (еще...)

Рассеяние - случайная величина

Cтраница 1

Рассеяние случайной величины относительно среднего принято характеризовать дисперсией.  [1]

Рассеяние случайной величины относительно среднего значения принято характеризовать дисперсией.  [2]

Характеристикой рассеяния случайной величины около ее математического ожидания служит дисперсия 0 случайной величины.  [3]

Мерой рассеяния случайной величины может служить: 1) среднее отклонение, 2) среднеквадратическое отклонение или же его квадрат - дисперсия, 3) средневероятное отклонение.  [4]

Характеристикой рассеяния случайной величины I, около ее математического ожидания служит дисперсия DI, случайной величины.  [5]

Дисперсией называют рассеяние случайной величины относительно среднего значения.  [6]

Дисперсия характеризует рассеяние случайной величины относительно математического ожидания.  [7]

Плотности веро - R ТРГ1Г1рТИ. пг ятности для нормального ширетч. pdo распределения с различ - четах для хар-к со-ным соотношением пара - противления малым метров. пластич. деформа.| Плотностьвероят - Д разрушения об-ности пределов текучести разца, N0 - порог as для стали марки Ст. 3. чувствительности ПО циклам, т. е. наибольшее количество циклов, для к-рого вероятность разрушения при N / V0 равна нулю. Для статистич. обработки результатов усталостных испытаний используются и другие распределения.  [8]

Для оценки рассеяния случайной величины пользуются также числовыми хар-ками, среди к-рых наибольшее значение имеют: 1) a - математич. Среднее значение и дисперсия являются параметрами нормального распределения. Перечисленные хар-ки носят название теоретич.  [9]

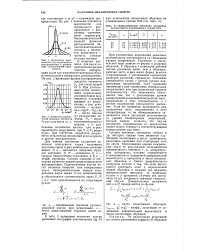
Плотности вероятности для нормального распределения с различным соотношением параметров.| Плотность вероятности пределов текучести as для стали марки Ст. 3.  [10]

Для оценки рассеяния случайной величины пользуются также числовыми хар-ками, среди к-рых наибольшее значение имеют: 1) а - математич. Среднее значение и дисперсия являются параметрами нормального распределения. Перечисленные хар-ки носят название теоретич.  [11]

Другой мерой рассеяния случайной величины, чаще употребляемой в практике, является среднеквадратическое отклонение.  [12]

Плотности вероятности для нормального распределения с различным соотношением параметров.| Плотность вероятности пределов текучести s для стали марки Ст. 3.  [13]

Для оценки рассеяния случайной величины пользуются также числовыми хар-ками, среди к-рых наибольшее значение имеют: 1) а - математич. Среднее значение и дисперсия являются параметрами нормального распределения. Перечисленные хар-ки носят название теоретич.  [14]

Плотности вероятности для нормального распределения с различным соотношением параметров.| Плотность вероятности пределов текучести as для стали марки Ст. 3.  [15]

Страницы:      1    2    3    4