Тривиальное расслоение

Cтраница 2

Ото - один из самых ранних примеров локально тривиальных расслоений, введенный X. [16]

Предложение 1.10. Если р: Е - В - локально тривиальное расслоение между компактными ориентируемыми многообразиями разных размерностей, OQ В, и если р - р, то Hm - n ( p - l ( bQ) 1i) ф 0; следовательно, МС р с ] не конечно. [17]

Мероморфная функция на компактном комплексно аналитическом многообразии определяет С локально тривиальное расслоение над дополнением к конечному подмножеству проективной прямой СР1 - бифуркационному множеству. Петлям вокруг точек бифуркационного множества соответствуют преобразования монодромии этого расслоения. В работе показывается, что дзета-функции этих преобразований монодромии могут быть выражены в локальных терминах, именно в виде интегралов дзета-функций мероморфных ростков по эйлеровой характеристике. Частным случаем мероморфной функции на проективном пространстве СР является функция, определяемая многочленом от п переменных. Описываются некоторые приложения данной техники к полиномиальным функциям. [18]

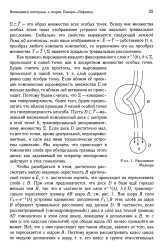Расслоение Милнора. [19]

Всюду вне множества особых точек наше отображение устроено как локально тривиальное расслоение. [20]

Действительно, ограничение касательного расслоения многообразия на его край изоморфно сумме одномерного тривиального расслоения и касательного расслоения края, т.е. стабильно эквивалентно последнему. Значение стабильного характеристического класса касательного расслоения многообразия на фундаментальном цикле края равно нулю, так как этот цикл гомологичен нулю. [21]

Расслоение ( В х F, В, prj) называется тривиальным расслоением с базой В и со слоем F. Изоморфизм расслоения К на три: виальное расслоение называется тривиализацией расслоения Я. [22]

Для вычисления фундаментальных групп групп Ли используют фрагмент точной гомотопической последовательности локально тривиального расслоения. [23]

Для того чтобы доказать, что ф является фактически проекцией некоторого локально тривиального расслоения, надо более тонко использовать лемму 4.3, чтобы получить более точное описание поведения p ( z) при z, стремящемся к множеству / С, на котором функция ф не определена. [24]

Итак, замена оператора Уд на деформированный оператор DA эквивалентна переходу от тривиального расслоения к расслоению L. [25]

Одно из обобщений заключается в замене категории векторных расслоений на категорию локально тривиальных расслоений, слоем к-рых является конечно порожденные модули, проективные над нек-рой С - алгеброй А, а структурные группы суть группы автоморфизмов этих модулей. С помощью этого класса расслоений построены нетривиальные когомологич. Если дискретная группа л является фундаментальной группой компактного многообразия, донус. [26]

Хорошо известно, что отображение F: С2 - С является локально тривиальным расслоением над дополнением к конечному множеству в образе С. Его слоем является общая кривая уровня Cgen многочлена F. C gen - преобразование монодромии этого расслоения, соответствующее петле 7 ( т) Дехр ( 2тггт) с достаточно большим вещественным R. Отображение h p называется преобразованием монодромии многочлена F на бесконечности. [27]

Многочлен Р, ограниченный на дополнение к гиперповерхности Н, определяет С локально тривиальное расслоение над дополнением к конечному подмножеству в С. Отсюда вытекает следующий результат. [28]

P ( z) / Q ( z) с являются слоями локально тривиального расслоения над проколотой окрестностью точки с. Оператор монодромии - это ( корректно определенное) действие соответствующего преобразования монодромии в группе гомологии слоя Милнора. [29]

Отображение B - BKG - получается сопоставлением с каждой единицей в - теории соответствующей ориентации на тривиальном расслоении. [30]

Страницы: 1 2 3 4