Значение - инвариант
Cтраница 3
Координаты критической точки - критическая температура Гкр, критическое давление pKV и мольный критический объем Vu - обычно удовлетворяют требованиям, предъявляемым к единицам пит, выбранным при вычислении значений инвариантов подобных систем. [31]
Полезно указать на различие между инвариантом подобия и множителем преобразования, в данном случае линейного, который иногда называют константой подобия. Значение инварианта подобия различно в разных точках системы, в то время как множитель преобразования остается постоянным. В самом деле, из подобия фигур, изображенных на рис. 3, следует, что диаметры второй системы по сечениям II и / / / будут соответственно dn 7 5 и dm 8 8, а первой системы d u 3 и d lu 3 5; множитель линейного преобразования остался неизменным. [32]
А именно, вычисляем для представителя ( / 3 0 / 4) значение этого инварианта для всех функций ( / 3 0 / 4) ( ж 0 a), a Е VQ, и проверяем найденные значения инвариантов на совпадение с теми, которые встречаются в табл. 7 у других представителей. Если значение инварианта для одной из функций ( / 3 0 / 4) ( х 0 а) при некотором а Е VQ совпадет со значением инварианта для некоторого другого класса эквивалентности, то их следует объединить в один класс. [33]
Весьма многочисленный вид составляют методы, основанные на вычислении и сравнении значений инвариантов для действия группы инерции G / на множестве векторов пространства Vn или на двойственном к нему пространстве линейных функций на Vn. После вычисления значений инвариантов и нахождения разбиения этого пространства, инвариантного относительно действия группы инерции, определяются запрещенные переходы векторов из разных классов этого разбиения друг в друга. Это позволяет получить ограничения на вид преобразований из группы инерции. В заключение, для каждого преобразования из этого множества производится проверка на принадлежность группе инерции. [34]
В результате получим наш торический узел, тривиальный узел и два трилистника. Согласно лемме 4.9 значение инварианта v3 на узле с двумя точками самопересечения полностью определяется его диаграммой Гаусса. [35]
В задачах, где требуется выяснить, можно ли с помощью ваданных операций перейти от одного из объектов к другому, часто полезно найти инвариант - числовую характеристику объектов ( или функцию с какими-то другими значениями на множестве объектов), которая не меняется при указанных операциях. Если при этом значение инварианта на двух объектах различно, то превратить один в другой нельзя. В целочисленных и других дискретных задачах инвариантом часто служит остаток от деления на 2 ( четность) или на другое натуральное число. [36]
Нетрудно убедиться, что вектор (2.17) действительно инвариант, при этом, как будет видно в дальнейшем, он не является точным. Другими словами, некоторым значениям инварианта (2.17) могут соответствовать не одна, а несколько неизоморфных блок-схем. Для тех величин and, которые встречаются на практике, их число обычно не превосходит четырех и поэтому задачу различения неизоморфных блок-схем в этом случае можно решить путем непосредственного перебора. [37]
Инварианты Римана постоянны вдоль соответствующих характеристик. В общем случае вдоль каждой характеристики одного семейства значения инварианта имеют свое значение. Инварианты Римана однозначно связаны с U и с, и их можно рассматривать как новые функции, описывающие течение. [38]
Тогда из соотношения (4.1) следует, что i / i ( fci) - vi ( k) Vi ( k2), где узел fca имеет две точки самопересечения. Таким образом, при заменах типов перекрестков узла i значение инварианта vi не изменяется. [39]
При доказательстве эквивалентности изложенный выше подход можно использовать только при наличии полной системы инвариантов, так как для нее из совпадения значений инвариантов следует принадлежность функций одному классу эквивалентности. Если же система инвариантов не полная, то из совпадения значений имеющихся инвариантов эквивалентность функций в общем случае не следует, и для доказательства эквивалентности приходится искать преобразование, переводящее одну функцию в другую. Сравнивая эти инварианты у обеих функций, можно получить ограничения на вид преобразований, которые могут переводить одну из функций в другую. [40]
 |
Комбинация методов дополнительных напряжений и Ньютоиа-Рафсоиа в механике закритического деформирования. [41] |
Проблема заключается в следующем. Поиск действительных значений инвариантов деформаций по полученным в очередном приближении значениям инвариантов напряжений в соответствии с методом дополнительных деформаций на стадии разупрочнения приводит к расхождению итерационной процедуры. Согласно же методу переменных параметров упругости, как и методу дополнительных напряжений, в каждом упругом решении положительному приращению инвариантов тензора деформаций соответствует положительное приращение инвариантов тензора напряжений, т.е. и на закритической стадии деформирования материал воспринимается как упрочняющийся, что не способствует сходимости. [42]
 |
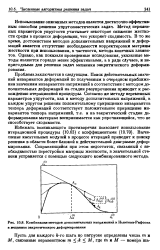
Направление С и С - характеристик в случае движения газа, ограниченного поршнем ( / и фронтом ударной волны ( 2. [43] |
Отсюда следует, что ( рис. 38) в любую находящуюся на поршне точку AJ переносится лишь вдоль С - характеристики инвариант J, образовавшийся в прошлом на фронте ударной волны. И, наоборот, С - характери-стика, унося с собой значение инварианта J, образовавшееся в точке А на поршне, уходит в будущее и спустя некоторое время Af / догоняет фронт ударной волны. Но в неоднородной среде ударная волна ускоряется. [44]
 |
Классификация функций от шести переменных относительно группы GL ( 6, 2 Е / з. [45] |
Страницы: 1 2 3 4