Молекулярный расчет

Cтраница 3

Задача теоретического расчета констант СТВ в радикалах решается в два этапа: во-первых, квантовохимический, молекулярный расчет, цель которого состоит в нахождении матрицы спиновой плотности, и, во-вторых, расчет изотропного СТВ и компонент тензора анизотропного СТВ с известной матрицей спиновой плотности. [31]

За исключением случая очень малых систем, неполнота базисного набора почти всегда является важнейшим источником погрешностей в молекулярных расчетах, а также в большинстве расчетов атомов, где используется алгебраическое приближение. Никакое расширение конфигурационного взаимодействия или суммирование членов высших порядков ряда возмущений не может компенсировать погрешности, связанной с неполнотой базисного набора. Результаты, полученные при полном учете конфигурационного взаимодействия в пространстве прямых произведений N-то ранга, генерируемого заданным базисным набором, могут по мере достижения полноты базисного набора лишь приближаться к результату полного учета конфигурационного взаимодействия. Выбор базисного набора в исследованиях атомных и молекулярных систем оказывает определяющее влияние на точность расчета. [32]

Этот важный и примечательный результат, характеризующий средние оптические свойства полимерного клубка - боба, - пе дает, однако, возможности молекулярного расчета. Модель свободно-сочлененной цепи не позволяет воспользоваться валентно-оптической схемой, так как исходит из рассмотрения статистических сегментов, а не реальных звеньев цепи. Тем не менее теория Купа и Грюна при переходе к сетке, к блочному полимеру дает цепные результаты. [33]

АО, обладающих приблизительно такой же точностью, как двухчленные ФСТ [21], найденные обычным методом Хартри-Фока и обеспечивающие достаточную надежность при проведении молекулярных расчетов. [34]

Но, к сожалению, нужно также отметить, что существует большое количество неясных и темных мест в такого рода общей интерпретации, возникшей на основе результатов самых простейших молекулярных расчетов. [35]

Кулоновский и обменный интегралы выражаются через атомные одноцентровые интегралы YAA ( легко определяемые по атомным спектрам) и двухцентровые кулоновские интегралы YAB, которые можно достаточно точно рассчитать на основе приближенных формул, как это делается в молекулярных расчетах при использовании приближения НДП. [36]

Необходимость оптимизации молекулярного базиса при расчете потенциальных кривых или в более общем случае - потенциальных поверхностей вызвана рядом причин, из которых наиболее существенной является изменение эффективного зарядового состояния атома в молекуле. В молекулярных расчетах полезно иметь в виду также и некоторые спектроскопические характеристики свободных атомов. В молекуле метана валентное состояние атома углерода может быть описано в рамках sp3 - гибридизованных орбиталей. Спектроскопическое состояние 55 свободного атома углерода, порождаемое конфигурацией sp3, известно. Валентное состояние атома в молекуле не совпадает с состоянием свободного атома. [37]

Остовные, валентная и псевдовалентные s - орбитали атома К. [38]

Кроме гладкой безузловой псевдовалентной орбитали строят и другие линейные комбинации. В молекулярных расчетах полезны такие псевдовалентные орбитали, которые малы в области остова. Критерии малости в области остова, так же как и критерии гладкости, могут быть разными. [39]

Кроме того, привлечение свойств молекулярной симметрии позволяет построить фоковскую матрицу в блок-диагональной форме, для которой проблема собственных значений может быть решена последовательно блок за блоком. При проведении молекулярных расчетов объем вычислений на стадии определения интегралов зависит от четвертой степени числа базисных функций, на стадии построения фоковской матрицы - также от четвертой степени числа базисных функций, а на стадии диагона-лизации этой матрицы - от третьей степени числа базисных функций. Стадия преобразования двухэлектронных интегралов к базисному набору двухэлектронных интегралов по молекулярным орби-талям зависит от пятой степени числа базисных функций, но и в этом случае учет молекулярной симметрии позволяет существенно снизить объем вычислений, необходимых для осуществления этого преобразования. Естественно, наибольшая эффективность достигается при условии, что базисные функции и молекулярные орбитали симметризованы относительно точечной группы симметрии молекулы. [40]

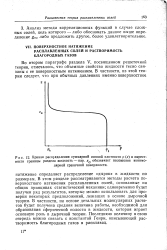Кривая распределения суммарной ионной плотности р ( z в окрестности границы раздела жидкость - пар. ZQ обозначает положение эквимо-лярной граничной поверхности. [41]

В этом разделе рассматриваются методы расчета поверхностного натяжения расплавленных солей, основанные на общих принципах статистической механики; одновременно будет получен ряд результатов, которые можно использовать для проверки некоторых предположений, лежащих в основе дырочной теории. В частности, на основе детальных молекулярных расчетов будет получена средняя величина работы, необходимой для образования сферической полости в жидкости, которая играет основную роль в дырочной теории. [42]

Здесь мы интересуемся главным образом изучением принципов, на которых основано проведение квантовохимических расчетов, а также выяснением того, как результаты этих расчетов применяются для объяснения химической связи и других химических явлений. При этом могут использоваться любые методы молекулярных расчетов. Однако большинство из них требует для изучения систем, представляющих химический интерес, использования электронно-вычислительных машин. Хотя практическая квантовая химия тесно связана с применением вычислительных машин, мы сосредоточим внимание на проблемах, цля решения которых вполне достаточно карманного калькулятора. Смысл такого подхода заключается в том, что лучший способ разобраться в чем-нибудь - это проделать все самому. [43]

Те из них, которые касаются молекулярных расчетов, - включены в книгу. [44]

Страницы: 1 2 3 4