Значение - сеточная функция
Cтраница 1
Значения сеточных функций, полученные на последней внешней итерации, отождествляются с результатом ( / 1) - го временного слоя. [1]
Для определения значений сеточной функции на сторонах многоугольника следует определить процедуру реконструкции. [2]
В данном случае значения сеточной функции вычисляются очень просто. [3]
 |
Алгоритм решения линейного уравнения переноса. [4] |
Полученная схема явная, поскольку значения сеточной функции в каждом узле верхнего слоя t tj i выражаются явно с помощью соотношений (8.28) через ранее найденные ее значения на предыдущем слое. [5]
 |
Последовательность четные узлы сетки, крестика-вычислений ми - граничные узлы, в кото. [6] |
На каждом слое последовательно вычисляются значения сеточной функции в узлах. [7]
Выражения (8.91) и (8.94) определяют значения сеточной функции во внутренних узлах, а решение на границе находится из граничных условий, которые зависят от конкретной постановки задачи. [8]
Отсюда последовательно получим, что все значения сеточной функции, отвечающей разности предполагаемых различных решений, равны нулю. [9]
Полученная схема - явная, поскольку значения сеточной функции в каждом узле верхнего слоя t ti l выражаются явно с помощью соотношений (8.36) через ранее найденные ее значения на предыдущем слое. [10]
Итерационный процесс контролируется максимальным отклонением М значений сеточной функции в узлах для двух последовательных итераций. Если его величина достигнет некоторого заданного малого числа е, итерации прекращаются и происходит вывод результатов. [11]
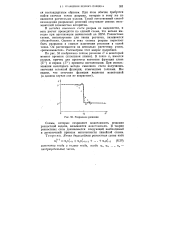 |
Разрывное решение. [12] |
При использовании некоторого метода сквозного счета получились значения сеточной функции, отмеченные точками. [13]
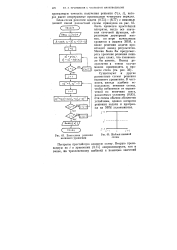 |
Блок-схема решения волнового уравнения.| Шаблон неявной схемы. [14] |
Здесь приведен простейший алгоритм, когда все значения сеточной функции, образующие двумерный массив, по мере вычисления хранятся в памяти ЭВМ, а после решения задачи происходит вывод результатов. [15]
Страницы: 1 2 3 4