Значение - волновая функция
Cтраница 1
Значения волновых функций на границах равны: я з ( 0) г э ( а) 0, и, следовательно, на ширине этой потенциальной ямы укладывается целое число полуволн. [1]
Соответствующая энергия определяется значением нормальной производной волновой функции на поверхности ядра. [2]
С другой стороны, значения волновых функций, описываю щих дырки, велики вокруг ионов теллура и серы, и поэтому форма потенциала внутри ионов влияет на вид этих функций. Эти волновые функции будут, очевидно, различными для ионов теллура и серы, и, таким образом, их разупорядочение оказывает сильное влияние на рассеяние дырок. [3]
С другой стороны, значения волновых функций, описывающих дырки, велики вокруг ионов теллура и серы, и поэтому форма потенциала внутри ионов влияет на вид этих функций. Эти волновые функции будут, очевидно, различными для ионов теллура и серы, и, таким образом, их разупорядочение оказывает сильное влияние на рассеяние дырок. [4]
В силу этого условия значение логарифмической производной волновой функции вне ядра не испытывает большого изменения на расстояниях порядка области диффузности ядерной поверхности. [5]
В табл. 2.1 приведено несколько значений волновой функции i W. Там же приведены графики радиальной функции и граничные поверхности, на которых § n i ml 2 const. С вероятностью 90 % электрон находится внутри граничной поверхности. [6]
Принцип Гюйгенса устанавливает связь между значением волновой функции в некоторой точке г и значениями волновой функции на замкнутой поверхности 5, окружающей эту точку. [7]
В свою очередь граничные условия задают значения волновой функции во все моменты времени на границах некоторой области пространства или на бесконечности. [8]
Дело при этом сводится к определению значения волновой функции ( решения соответствующего уравнения Шредингера) при нулевой энергии в начале координат. [9]
Это иллюстрирует рис. 6.1, где приведены значения волновых функций вдоль линии, соединяющей ядра, и дано их сопоставление с точными результатами. Из рисунка видно, что в la - состоянии волновая функция, найденная в ЛКАО-приближении, имеет на ядрах значения, заниженные по сравнению с точными, а в 1ты - со-стоянии - завышенные. [10]
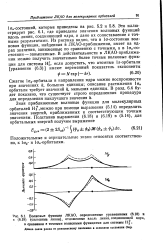 |
Волновые функции ЛКАО, определяемые уравнениями и и ( сплошные линии, отложенные вдоль линии соединяющей ядра. [11] |
Это иллюстрирует рис. 6.1, где приведены значения волновых функций вдоль линии, соединяющей ядра, и дано их сопоставление с точными результатами. Из рисунка видно, что в la - состоянии волновая функция, найденная в ЛКАО-приближении, имеет на ядрах значения, заниженные по сравнению с точными, а в 1 Си-состоянии - завышенные. [12]
Поскольку программа ГАРМ позволяет рассчитать также зависимость значения волновой функции от смещения атомов от равновесного положения, можно изобразить эту зависимость в виде графика на миллиметровой бумаге. Однако следует иметь в виду, что отклонение волновой функции от нуля при больших межъядерных расстояниях связано с приближенным характером численного метода решения уравнения Шредингера. При большой амплитуде колебаний даже небольшое изменение энергии вызывает уход волновой функции в оо или - оо. При построении графиков эти значения лучше всего не учитывать и считать, что в этих точках волновая функция имеет нулевое значение. [13]
Рациональные числа ( главным образом натуральные), определяющие физически осуществимые значения волновой функции квантовой системы. [14]
Оператор 5г зависит от представления S, по которому преобразуется пространство L значений волновой функции. Наоборот, оператор М3 не зависит от представления S. В том частном случае, когда волновая функция ф является скаляром, представление S является единичным, оператор 5г равен нулю, а оператор проекции орбитального момента М, совпадает с оператором проекции полного момента J. Таким образом, различие между операторами Mz и J2 возникает только в тех случаях, когда пространство L преобразуется по представлению группы вращений более сложному, чем единичное представление. [15]
Страницы: 1 2 3 4