Значение - волновая функция
Cтраница 3
Молекулярная орбиталь, образующаяся при подобном взаимодействии, характеризуется уменьшением абсолютной величины волновой функции в межъядерном пространстве по сравнению с ее значением в исходных атомах: на оси связи появляется даже узловая точка, в которой значение волновой функции, а, следовательно, и ее квадрата, обращается в нуль. Это означает, что в рассматриваемом случае уменьшится и плотность электронного облака в пространстве между атомами. Здесь, следовательно, химическая связь не возникает; образовавшаяся в этом случае МО называется разрыхляющей ( сг), а находящиеся на ней электроны - разрыхляющими электронами. [31]
Иногда утверждают, что основной вклад в матричные элементы оператора спин-орбитального взаимодействия дает область вблизи ядра центрального иона, где - а) потенциальная энергия V ( r ] практически равна энергии V ( r) свободного иона и б) значения волновых функций лигандов, примешанных к молекулярным орбиталям табл. 24, малы. [32]
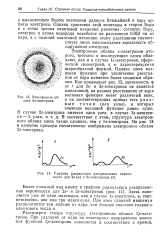 |
Электронное облако 2-электрона.| Графики радиального распределения вероятности для 2s - ( a и Зз-электронов ( б. [33] |
Как показывает рис. 12, зависимость тр от г для 2s - и Ss-электронов не является монотонной, на разных расстояниях от ядра волновая функция имеет различный знак, а на соответствующих кривых есть у з л о вые точки ( или узлы), в которых значение волновой функции равно нулю. [34]
Здесь 4a ( v) - сечение двуквантовой аннигиляции и позитрона, имеющих общий спиновый момент, равный нулю; G ( V) - усредненное по спинам сечение аннигиляции, вычисленное Дираком; 4 учитывает статистические веса состояний с моментом 0 и 1; ) ( 0) - значение волновой функции позитрония в начале координат в основном состоянии; v - скорость. [35]
Разные свойства синглетного и триплетного состояний количественно определяются значениями обменного интеграла А. Поскольку значения волновых функций экспоненциально убывают на больших расстояниях, то на больших расстояниях значение А экспоненциально уменьшается с расстоянием. [36]
В связи с тем, что взаимодействующие молекулы находятся на несколько больших расстояниях, выбор правильной волновой функции представляет очень трудную задачу. Во-первых, значения волновой функции в этой области малы, что предъявляет особые требования к точности ее определения. На таких расстояниях часто играют роль не валентные орбитали, а внешние, вакантные в основном состоянии орбитали. Во-вторых, межмолекулярные взаимодействия по своей природе являются многочастичными и необходимо рассматривать сразу крупные объединения частиц - их ансамбли. Причем каждая из частиц должна быть определенным образом расположена и ориентирована в пространстве. Это резко увеличивает объем вычислительной работы. Наконец, теоретические и расчетные методы еще не позволяют при современном уровне развития вычислительной техники получить достаточно точное решение. Для обеспечения притяжения молекул особое значение приобретает корреляция электронов. Под корреляцией электронов понимают такое коллективное движение, когда они как бы стараются избегать друг друга и больше находиться в поле положительного заряда. Корреляция электронов представляет собой самостоятельную и сложную задачу квантовой химии. Поэтому теоретические квантово-химические методы в настоящее время используются наряду с подходами, основанными на законах классической физики. [38]
Волновая функция наиболее низкого уровня, или орбитальная, для водородного атома обладает сферической симметрией. Другими словами, значение волновой функции зависит только от расстояния, но не от направления. По историческим причинам эта функция обозначается как орбита Is атома водорода. Часто ее схематически изображают в виде шара с рыхлой поверхностью, для того чтобы обозначить отсутствие резкой границы. Ближайшая по уровню орбита тоже обладает сферической симметрией и известна как - орбита. Ближайшие три функции называются 2р - орбитами. Они имеют ту же самую энергию, что и 25-орбиты. Эти р-функции симметричны относительно трех перпендикулярных осей. Каждая орбита имеет три квантовых числа, описывающих те части волновой функции, которые определяют расстояния от ядра и два угла, необходимые, чтобы определить точку в пространстве. На рис. 5.6 приведено схематическое изображение s - и р-орбит. [39]
Волновая функция наиболее низкого уровня, или орбитальная, для водородного атома обладает сферической симметрией. Другими словами, значение волновой функции зависит только от расстояния, но не от направления. По историческим причинам эта функция обозначается как орбита is атома водорода. Часто ее схематически изображают в виде шара с рыхлой поверхностью, для того чтобы обозначить отсутствие резкой границы. Ближайшие три функции называются 2р - орбитами. Они имеют ту же самую энергию, что и 2 -орбиты. Эти р-функции симметричны относительно трех перпендикулярных осей. Каждая орбита имеет три квантовых числа, описывающих те части волновой функции, которые определяют расстояния от ядра и два угла, необходимые, чтобы определить точку в пространстве. На рис. 5.6 приведено схематическое изображение s - и р-орбит. [40]
 |
Энергия свободного электрона в приведенной зоне. [41] |
Выделим мысленно в кристалле макроскопический объем V в форме куба с ребром L, причем ребра направим из начала координат вдоль координатных осей. Потребуем теперь совпадения значений волновой функции на противоположных гранях куба и будем представлять бесконечный кристалл, составленным из таких кубов, так что волновая функция непрерывно переходит из каждого объема в соседний. Естественно считать, что объем V совпадает с объемом реального кристалла. [42]
 |
Модель потенциальной ямы. [43] |
Мы предполагаем, что электрон свободно движется вдоль отрезка длиной. При бесконечно большом U значение волновой функции электрона т з должно равняться нулю и, следовательно, перемещение электрона ограничено. [44]
В яме бесконечной глубины волновая функция на границах ямы ( х0 и х1) равна нулю. Так как на рисунке значения волновой функции на границе отличны от нуля, то, следовательно, глубина потенциальной ямы конечна. [45]
Страницы: 1 2 3 4
