Нелинейный резонанс

Cтраница 1

Нелинейный резонанс является важным свойством динамических систем, характеризующим их реакцию на внешнее возмущение и позволяющее оценить роль нелинейности. [1]

Нелинейные резонансы при k N, возможные для первой области устойчивости уже при kx - - -) - kz 3, проявляются даже в идеальном ноле без низкочастотных гармоггик искажения ноля. Даже вдали от такого резонанса может существовать продельная амплитуда бетатронных колебаний, превышение к-рой приводит к дефокусировке. [2]

Рассмотренный нелинейный резонанс показывает, что даже очень малые возмущения могут приводить к сильным изменениям в системе. И хотя эти изменения могут быть относительно малы по величине, они могут создавать сильные качественные изменения в свойствах системы. [3]

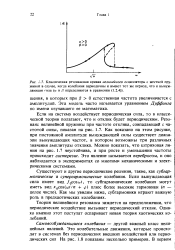Классическая резонансная кривая нелинейного осциллятора с жесткой пружиной в случае, когда колебания периодичны и имеют тот же период, что и вынуждающая гила ( а и ft определяются в уравнении. [4]

Теория нелинейного резонанса зиждется на предположении, что периодическое воздействие вызывает периодический отклик. Однако именно этот постулат оспаривает новая теория хаотических колебаний. [5]

Сам по себе нелинейный резонанс может и не приводить к гибели частиц, однако при этом возрастает поперечный размер пучка, что уменьшает светимость. [6]

В, Взаимодействие нелинейных резонансов - Новосибирск: Изд. [7]

Для медленного вывода обычно используется нелинейный резонанс 3-го порядка Qrm / 3, возбуждаемый m - ii гармоникой квадратичной нелинейности маги. [8]

При максимальном демпфировании кривые для нелинейного резонанса практически совпадают с характеристикой / линейной системы. [9]

Фурье) при выполнении условий нелинейного резонанса, обсуждаемых в гл. [10]

Во вращающейся системе фазовые портреты нелинейного резонанса для двух случаев представлены на рис. 2.1 и 2.2. Из них, в частности, видно, что при резонансе порядка / 0 на фазовой плоскости образуются / 0 сепаратрисных ячеек, / 0 гиперболических и / о эллиптических особых точек. Таким образом, нелинейный резонанс изменяет топологию фазового портрета. [11]

Установим некоторые условия захвата системы в нелинейный резонанс. [12]

Рассмотрим вопрос о стохастизации лучей в неоднородных средах вследствие нелинейного резонанса. [13]

В § 2.1 и 2.2 было рассмотрено очень важное явление нелинейного резонанса между системой и внешним возмущением или между внутренними степенями свободы системы. Среди упрощений, используемых для его анализа, содержится одно, которое будет обсуждено здесь. Речь идет о пренебрежении нерезонансными членами. Это настолько обычное в современной физике приближение, что трудно найти такую область, где бы оно не применялось. В действительности именно учет нерезонансного члена приводит к малому, но качественно новому результату - к образованию стохастического слоя на месте сепаратрисы нелинейного резонанса. Ширину этого слоя можно записать практически сразу, используя уже готовые результаты. [14]

Схема резонаисов показана на рис. 4, где сплошными линиями отмечены линейные, а пунктирными - нелинейные резонансы. Физический смысл нелинейных резонансов довольно прост: вторая гармоника попадает на одну из собственных Рда - 4 Схеш резонансов конечных частот ( линейных peso - колебаний трубы. [15]

Страницы: 1 2 3 4