Аналог - условие
Cтраница 2
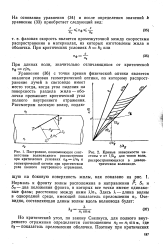
Уравнение ( 36) с точки зрения физической оптики является аналогом условия геометрической оптики, по которому распространение лучей в световоде имеет место тогда, когда угол падения на поверхность раздела жила - оболочка превышает критический угол полного внутреннего отражения. [17]
Необходимые условия слабого минимума б / 0, 6Vi0 являются точными аналогами условий минимума / ( ж) 0, / ( х) 0 для функций одного переменного. Условие Якоби при выполнении Лежандра условия ( усиленного) является необходимым условием неотрицательности второй вариации. [18]
Рассматривается задача поиска минимума для класса скалярных функций, удовлетворяющих некоторому вероятностному аналогу условия Липшица. Изучаются оптимальные байесовы алгоритмы. [19]
Для такой системы теорема Фробениуса об интегрируемости n - мерного распределения - пересечения всех косимметрии - является аналогом условия инволютивности первых интегралов в гамильтоновом случае. [20]
В § 0.7 мы видели, что свободную ассоциативную алгебру k X на множестве X над полем k можно определить как полугрупповую алгебру свободной полугруппы Sx над k слабый алгоритм, выполняющийся в свободной алгебре, можно считать аналогом условия ( iii) теоремы 6.1. Используя эту теорему, мы покажем, что однородные элементы алгебры k X образуют свободную полугруппу. В дальнейшем будем считать множество X линейно упорядоченным и упорядочим одночлены от X разной длины по их длине, а одночлены одинаковой длины-лексикографически. [21]
Таким образом, условие Якоби заключается в том, что интервал ( t0, tj) не должен содержать точек, сопряженных с 0 - Необходимые условия слабого минимума 670, SV O ( условия Лежандра) являются точными аналогами условий минимума f ( x) Q, / ( z) 0 для функций одного переменного. Условие Якоби при выполнении условия Лежандра ( усиленного) является необходимым условием неотрицательности второй вариации. [22]
Условие (5.157) эквивалентно требованию, чтобы гессова матрица H ( q) была положительно определенной по всей области допустимых значений вектора Д / в параметрическом пространстве. Одномерным аналогом условий (5.155) и (5.157) являются известные условия, в соответствии с которыми в точке минимума функции первая производная отсутствует, а вторая производная положительна. [23]
А степени 0 и при заданной линии R определяется на пересечении ILj П R. Это нелинейный аналог условия типа (6.10.59), при котором коцикл является кограницей. [24]
Соотношения (3.21) и (3.22) называются теоремой взаимности. Она является аналогом условия симметрии функции Гри-иа в скалярном случае. Согласно этой теореме, можно менять местами положение точки наблюдения и источники поля, что используется при решении многих практических задач, в частности при расчете антенн. [25]
Кроме того, предполагается, что-при достаточно больших х производная Qx отрицательна. Это условие является аналогом условия отрицательности кривизны в проблеме геодезических исследований, к которой применены методы символической динамики. На физическом языке уравнение ( 1) описывает движение частицы в одномерной потенциальной яме, профиль которой периодически меняется со временем. Другими словами, система испытывает периодические возмущения, которые и вызывают резонансные явления. Существенным для дальнейшего рассмотрения является сильная нелинейность задачи. Как известно, период линейных колебаний не зависит от амплитуды, в то время как в рассматриваемых нами случаях он должен расти и притом достаточно быстро. [26]
Почти симплектическое ( почти комплексное) подмногообразие S С V симплектического ( комплексного) многообразия I /, очевидно, наследует интегрируемую симплектическую ( комплексную) структуру. Заметим, что в случае римановых многообразий это не так: аналогом условия интегрируемости здесь является условие локальной евклидовости, однако подмногообразия локально евклидовых многообразий, конечно, не обязаны быть локально евклидовыми. [27]
Ограничение (28.25) сравнительно жесткое; при пространственном шаге 300 км, использованном Чарни и Филлип-сом [1953], стр. Таким образом, 24-часовой прогноз требует около 24 шагов по времени, каждый из которых включает решение краевой задачи для уравнения Пуассона. Было бы весьма желательно найти какой-нибудь способ допускать более длинный интервал по времени К. Условие (28.25) является аналогом условий (7.7) и (26.12), выведенных раньше. [28]
Одним из основных методов представления знаний в CLIPS являются правила. Правила используются для представления эвристик, определяющих ряд действий, которые необходимо выполнить в определенной ситуации. Разработчик экспертной системы определяет совокупность правил, которые используются совместно для решения проблемы. Правило состоит из двух частей: антицедента ( условия), который является аналогом условия в if-then операторе и записывается слева, и консеквента ( заключения), который является аналогом then части этого оператора и записывается справа. [29]
Центральным результатом, устанавливающим такую связь, является доказанная в § 7 теорема об изоморфизме. В главе 4 на примере пространств гладких функций рассмотрены некоторые эффекты, возникающие при изучении функциональных операторов в других пространствах. В главе 5 приведены приложения к дифференциально-функциональным уравнениям, псевдодифференциальным и сингулярным интегральным уравнениям со сдвигом, нелокальным краевым задачам, уравнениям типа свертки и другим вопросам. Среди результатов этой главы наиболее важными представляются конструкции символа дифференциально-функционального оператора с частными производными и аналог условия Лопатинского для нелокальных краевых задач. В § 20 получены формулы индекса для некоторых из рассматриваемых операторов. [30]
Страницы: 1 2