Собственное значение - уравнение
Cтраница 2
Поэтому в первую очередь следует найти собственные значения уравнения Шредингера для данной механической задачи, которые являются выделенными уровнями энергии. Соответствующие собственные функции в противоположность собственным значениям имеют второстепенный интерес. [16]
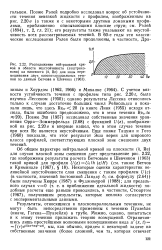 |
Расположение нейтральной кривой в области неустойчивости ( заштрихована на плоскости ( &, Re для зоны перемешивания двух плоскопараллельных течений по данным Бетчова и Шевчика ( 1963. [17] |
Позже Эш ( 1957) исследовал собственные значения уравнения Орра-Зоммерфельда (2.68) с функцией U ( z), изображенной на рис. 2.20 в и впервые нашел, что в этом случае течение при всех Re является неустойчивым. Еще позже Тацуми и Гото ( 1960) показали, что этот результат Эша верен для широкого класса профилей, соответствующих плоской зоне смешения двух течений. [18]
Заметим лишь, что первые пять собственных значений уравнения ( 21 33) могут быть указаны сразу. [19]
Доказательство леммы 3.1. Если jw, - собственные значения уравнения (2.1) для условий (3.11), то ip ( t, / -) - собственные функции. [20]
Последняя лемма справедлива, даже если некоторые собственные значения уравнения (10.1.1) лежат на мнимой оси. Легко проверить, что пригодно - то же самое доказательство. [21]
В этом параграфе рассмотрен случай, когда собственные значения уравнения (41.2) являются невырожденными и гамильтониан не зависит от времени. [22]
Хеммерлину [10] удалось строго математически решить задачу собственных значений уравнений возмущающего потока. [24]
Для колебаний с фиксированной частотой Л, есть собственное значение уравнения (8.5.76), совпадающего с (8.5.36), но теперь уже а фиксированно. [25]
Обобщенные волновые сфероидальные функции, определяющие собственные функции и собственные значения уравнений (3.27), находят все большее приложение в технике. [26]
Нулевым приближением в этой задаче являются собственные функции и собственные значения уравнения Шредингера для электрона в атоме водорода. [27]
Для свободных волн, однако, та получается, как собственное значение уравнения (8.5.20) с соответствующими граничными условиями. [28]
Согласно закону 3, всякое повторное измерение дает одно из собственных значений уравнения ( III. [29]
Следовательно, чтобы правильно определить энергию связи электрона на г - й спин-орбитали, нужно вычислить собственное значение уравнений Хартри-Фока - Слейтера для гипотетического переходного состояния, в котором на i - й спин-орбитали находится 1 / 2 электрона. [30]
Страницы: 1 2 3 4