Первое собственное значение

Cтраница 2

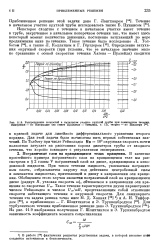Распределение скоростей в начальном участке круглой трубы при ламинарном течении. Измерения - по Никурадзе ( из книги Прандтля - Титьенса, т. II, теория - по Шиллеру. [16]

Для этой задачи были вычислены пять первых собственных значений. По Толботу при числе Рейнольдса Re Ю3 окружная скорость почти полностью затухает на расстоянии сорока диаметров трубы от входного сечения, что хорошо совпадает с результатами эксперимента. [17]

Эта формула позволяет вычислить поправки к первому собственному значению за счет присоединенного объема. [18]

В сравнении с оценкой (41.13) эта оценка для первого собственного значения лучше; оценки второго и третьего собствен ных значений очень грубы. [19]

Теорема включения в случае частных задач на собственные значения для первого собственного значения доказана в работе О. [20]

Последовательные итерации вектора g матрицей а. [21]

Так как матрица a - симметрическая, то для вычисления ее первого собственного значения используем метод скалярных произведений. [22]

При п - оо (21.9) переходит в соответствующее минимальное выражение для первого собственного значения задачи (21.7) ( ср. [23]

Из формул (24.23) видно, что все резонансы заключены только в первом собственном значении ро, так как только оно зависит от частоты. [24]

Функционал (4.3.32) при условии (4.3.33) имеет единственный минимум, значение которого дает первое собственное значение Vj, а функция i № ( M), на котором этот минимум достигается, является соответствующей собственной функцией задачи. [25]

Функционал (4.35) при условии (4.36) имеет единственный минимум, значение которого дает первое собственное значение IHj, а функция и ( г) ( M), на котором этот минимум достигается, является соответствующей собственной функцией задачи. [26]

Грина порождает вполне непрерывный интегральный оператор, причем одно или несколько его первых собственных значений оказываются простыми. Тогда фредгольмовским будет и оператор В, и числа нулей В и задачи (35.3) совпадают. [27]

Все обобщенные решения неравенства (2.2), (2.3) неотрицательны тогда и только тогда, когда первое собственное значение задачи (2.12) положительно. [28]

Для рассматриваемой конкретной задачи, как и вообще для задач устойчивости, непосредственный практический интерес представляет только первое собственное значение, дающее значение критической силы, и первая собственная функция, описывающая форму потери устойчивости. Остальные собственные функции могут быть полезны для построения приближенных решений более сложных задач с теми же граничными условиями. [29]

Для того чтобы функционал (6.2) был положительно-определенным в пространстве Е, необходимо и достаточно, чтобы первое собственное значение задачи (6.6), (6.7) было положительным. [30]

Страницы: 1 2 3 4