Бифуркационное значение - параметр
Cтраница 1
Бифуркационные значения параметров ch в плоскостях сечений определяются следующим образом. [1]
Бифуркационное значение параметра называется регулярным, если ему соответствует ровно одна бифуркационная точка, и притом невырожденная. [2]
Бифуркационные значения параметров можно найти, если заметить, что кривые N ( ( p, vuQ, vc0) 0 в точках бифуркации имеют вертикальную касательную. [3]
Последовательность бифуркационных значений параметра, соответствующих выходу в комплексную область мультипликаторов цикла периода 2, возникающего в каскаде удвоений, имеет вид en c6 - n O ( 6 - naK), где б - константа Фейгенбаума, сг - максимальное сжимающее собственное значение линеаризации оператора удвоения в неподвижной точке G, с - константа, зависящая от семейства. [4]
При другом бифуркационном значении параметра р р2 неустойчивый предельный цикл стягивается в особую точку, которая становится неустойчивой. [5]
При прохождении бифуркационного значения параметра сепаратрисы обеих седел меняются местами. [6]
Так как бифуркационными значениями параметра К могут быть только те значения, при которых линеаризованное уравнение имеет ненулевые решения, то 0 является изолированным бифуркационным значением. [7]
 |
Бифуркация петли сепаратрисы, предельной для Сепаратрисы Другого седла. При е0 показан момент возникновения седловой связки. [8] |
Однопараметрическая деформация соответствующей бифуркационному значению параметра системы, определенная типичным семейством, при значениях параметра, близких к бифуркационному, топологически нереальна и структурно устойчива: любая другая деформация топологически эквивалентна индуцированной из данной, любая близкая однопараметриче-ская деформация топологически эквивалентна данной. [9]
Как известно [9], бифуркационное значение параметра определяется условием перехода собственного значения линеаризованной задачи через нуль или мнимую ось. [10]
В других случаях при бифуркационном значении параметра сразу возникает предельный цикл с конечной амплитудой - окесткое зарождение предельного цикла. [11]
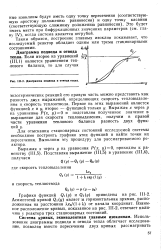 |
Диаграмма подвода и отвода тепла. [12] |
Это будет иметь место при бифуркационных значениях параметров ( см. главу IV), когда система является негрубой. [13]
Для однопараметрических семейств общего положения все бифуркационные значения параметра регулярны. Если фазовое пространство компактно, то бифуркационные значения параметра изолированы. [14]
 |
Фазовые портреты уравнения. [15] |
Страницы: 1 2 3 4