Аддитивность - энтропия
Cтраница 2
Из предыдущего анализа логически вытекает свойство аддитивности энтропии: энтропия системы равна сумме энтропии тел, составляющих систему. [16]
В равной мере здесь возможен подход и к аддитивности энтропии активации. Это было отмечено ранее Тротманом-Дикенсо - ном [140], а Березиным [141 ] проведены также расчеты энтропии активации и гиббсовой энергии активации для некоторых радикальных реакций. [17]
Неизменность Д5298 для данной группы соединений соответствует правилу аддитивности энтропии Капустинского и Яцимирского. [18]
Неизменность AS s Для данной группы соединений соответствует правилу аддитивности энтропии Капустинского и Яци-мирского. [19]
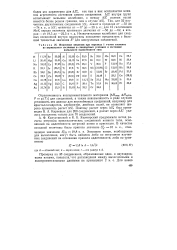 |
Изменение энтропии при переходе 1 г-атом элемента. [20] |
Ядимирский предложили метод расчета энтропии кристаллических соединений ионного типа, основанный на аддитивности энтропии ионов в кристалле. [21]
Свойство энтропии независимых распределений складываться при объединении этих распределений в одной называется свойством аддитивности энтропии. [22]
Закономерность, наблюденная Киреевым, однако, является частным случаем, вытекающим из правила аддитивности энтропии в форме, изложенной в этом разделе. [23]
Для более сложных систем, где возможен массообмен между их частями, надо особо доказать аддитивность энтропии, что всегда можно сделать аналогично изложенному. Но мы не прослеживаем далее построение термодинамического формализма, так как нас интересует только принципиальная сторона дела. [24]
Капустинский и Яцимирский [313] недавно предложили метод расчета энтропии соединений ионного типа, основанный на аддитивности энтропии ионов. [25]
Для неидеал ьногазовых систем ( жидкости, твердые тела) самым специфическим свойством является нарушение аддитивности энтропии. Термодинамические вероятности частей системы в этом случае не являются независимыми и поэтому не подлежат просто умножению при определении вероятности состояния системы в целом. Нам остается только догадываться, что отклонение энтропии от аддитивности для реальных систем строго соответствует отклонению термодинамической вероятности системы в целом от произведения вероятностей ее частей. Для принятия такого рода гипотезы имеется немало оснований, что показал Гиббс, анализируя некоторые аналогии между уравнениями термодинамики и статистики. Однако не исключена возможность, что мотивировке Гиббса может быть придан иной смысл, вследствие чего в соотношения, которые в данный момент являются общепризнанными, придется, быть может, внести некоторые существенные коррективы, чтобы они сохранили точность для реальных систем. [26]
Таким образом, тождественность формул ( 2) и ( 3) доказана и тем самым доказана аддитивность энтропии для случая смешения газов. [27]
А Ф Капустинский и К Б Яцимирский предложили метод расчета энтропии кристаллических соединений ионного типа, основанный на аддитивности энтропии ионов в кристалле. [28]
Получим теперь некоторые соотношения, связывающие энтропию системы со значениями энтропии подсистем, т.е. вернемся к обсуждению вопроса об аддитивности энтропии. [29]
Перейдем к свойствам энтропии, которые являются специфическими для логарифмической, функции, а именно, к свойствам, связанным с аддитивностью энтропии. [30]
Страницы: 1 2 3 4