Произвольное возмущение

Cтраница 1

Произвольное возмущение может быть разложено по полному набору нормальных колебаний. [1]

Произвольное возмущение может содержать составляющие как высокой, так и низкой частоты. Низкочастотные составляющие будут идти с меньшей скоростью, близкой к Се: затухая значительно слабее. [2]

Произвольное возмущение может содержать составляющие как высокой, так и низкой частоты. Высокочастотные составляющие ( со 1) будут распространяться со скоростью, близкой к максимально возможной и равной Cf d, при этом будут быстро затухать. Низкочастотные составляющие будут идти с меньшей скоростью, близкой к Се, затухая значительно слабее. Так как выражение k % ( со) очень громоздкое, то имеет смысл предварительно аппроксимировать зависимости С ( со) и k % % ( со) более простыми выражениями. [3]

Для произвольного возмущения F, F ( x, t) Q, t0, могут иметь место либо принцип Гюйгенса, либо диффузия волн, либо их наложение. Физические интерпретации и геометрические построения аналогичны рассмотренным в § 14.2 и § 14.3 соответственно. [4]

Для произвольного возмущения F, F ( x, t) Q, t 0, могут иметь место либо принцип Гюйгенса, либо диффузия волн, либо их наложение. Физические интерпретации и геометрические построения аналогичны рассмотренным в § 14.2 и § 14.3 соответственно. [5]

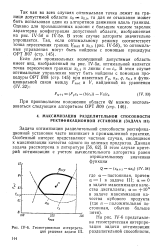Геометрическая иитерпрета-ция решения задачи III. [6]

Если для произвольных возмущений допустимая область имеет вид, изображенный на рис. IV - 5e, оптимальной является точка пересечения границы xQi 3 и линии с сэ. В этом случае оптимальные управления могут быть найдены с помощью процедуры ОРТ В08 ( стр. [7]

Если для произвольных возмущений допустимая область имеет вид, изображенный на рис. IV-50. В этом случае оптимальные управления могут быть найдены с помощью процедуры ОРТ Б08 ( стр. [8]

Таким образом, произвольные возмущения при R Ri затухают. Иначе говоря, в подкритической области не существует никаких других стационарных решений нелинейных уравнений, кроме равновесного. [9]

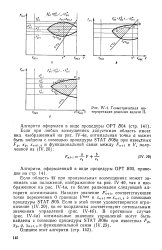Геометрическая ин-терпретация решения задачи II. [10]

Если область LL при произвольных возмущениях может занимать как положение, изображенное на рис. IV-46, так и изображенное на рис. IV-40, то более рационален следующий алгоритм оптимизации. Если в этой точке удовлетворяется ограничение ( IV. [11]

Геометрическая интерпретация решения задачи II. [12]

Если область U при произвольных возмущениях может занимать как положение, изображенное на рис. IV-46, так и изображенное на рис. IV - 4s, то более рационален следующий алгоритм оптимизации. Если в этой точке удовлетворяется ограничение ( IV. [13]

Можно, однако, разложить произвольное возмущение на такие части, каждая из которых распространяется лишь по одной из характеристик. [14]

Можно, однако, разложить произвольное возмущение на такие части, каждая из которых рас-лространяется лишь по одной из характеристик. [15]

Страницы: 1 2 3 4