Электронная волна

Cтраница 2

Рассеяние электронных волн может происходить не только на резких неоднородностях электрического поля, вызванных флуктуациямп теплового движения ионов решетки, но и на еще более резких искажениях поля, создаваемых посторонними ионами примеси. Если число таких ионов велико, как это имеет место в сплавах, представляющих собой твердые растворы, то подвижность электронов и электропроводность уменьшаются. Как правило, сплавы металлов обладают большим удельным сопротивлением и меньшим температурным коэффициентом, чем чистые металлы. [16]

Рассеяние электронных волн имеет в полупроводниках такое же происхождение, как и в металлах. Но в то время как в металлах электронные волны, имеющие длину порядка междуатомных расстояний, рассеиваются на основных атомных колебаниях, в 20 раз более длинные электронные волны в полупроводниках рассеиваются преимущественно на более медленных колебаниях кристаллической решетки, которых значительно меньше. [17]

Рассеяние электронных волн, а следовательно, величина подвижности и и ее зависимость от температуры в этих случаях количественно отличны от рассеяния электронов в металлах. [18]

Свойства электронных волн мы рассмотрим только в таком объеме, какой необходим для наших целей. Мы уже раньше обсуждали одно из важнейших ее свойств, а именно - соотношение между длиной волны и скоростью электрона. Она представляет синусоидальную функцию пространственных координат или функцию подобного типа, периодическую или приближающуюся к периодической. Она может быть и функцией времени, и в этом случае она является периодической функцией времени. [19]

Рассеяние электронной волны на дефектах решетки и примесях также приводит к потере электронами энергии, накопленной в электрическом поле. Эта энергия превращается в энергию колебательного движения атома примеси или другого дефекта, а от него передается всей решетке, из-за чего, в конечном счете, число фононов тоже увеличивается. [20]

Электронное облако с ности нахождения электрона, т. е. оп-неравномерной плотностью ределяется величиной Hf ( при полном. [21]

Движение электронной волны количественно характеризуется амплитудой г), находимой из дифференциального уравнения Шредин-гера. [22]

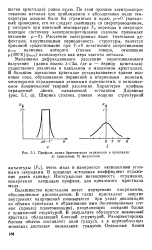Профиль линии брэгтовского отражения в кристалле. а идеальном. б мозаичном. [23]

Рассеяние электронных волн точечными дефектами, нарушающими периодичность структуры, является причиной существования при T - Q остаточного сопротивления рост, величина которого ( точнее говоря, отношение р ( 300Ю / РОСТ) используется как мера чистоты металла. [24]

Длина электронной волны X вычисляется из величины ускоряющего потенциала с помощью соответствующей формы уравнения де - Бройля ( стр. Напряжение измеряется вольтметром любой системы, прокалибрированным с помощью электронограммы золотой фольги, расстояния для которой точно известны благодаря измерениям рентгеновскими лучами. [25]

При этом электронная волна будет частично отражаться от стенок каждой потенциальной ямы. Отраженные волны уносят часть энергии прямой волны, ослабляя ее. [26]

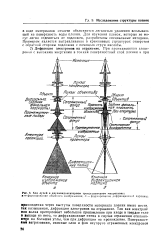Ход лучей в двухконденсаторном трехступенчатом микроскопе. [27]

Так как электронная волна претерпевает небольшое преломление при входе в твердое тело и выходе из него, то дифракционные пятна в случае отражения отклоня-ются на большие углы, чем при дифракции на прохождение. [28]

При этом электронная волна разлагается на ряд гармоник, соответствующих различным значениям квантованного момента количества движения электрона относительно рассеивающего центра поля атома. [29]

Рассеяние же электронных волн на упругих волнах кристалла снова удобно рассматривать на корпускулярном языке, используя картину столкновений корпускул двух типов - электронов и фононов. Хорошим примером условного моделирования служит также образ электронного облака, используемый для электрона в атоме. Как видите, моделирование в квантовой механике используется достаточно широко и гибко. При этом все модели понимаются не буквально, а УСЛОВНО, относительно. [30]

Страницы: 1 2 3 4