Гармоническая волна

Cтраница 2

Если скорость гармонической волны не зависит от частоты ( зависимость и от k является линейной, т.е. отсутствует дисперсия), то такому же уравнению удовлетворяет любая суперпозиция плоских волн. [16]

Зависимость скорости гармонической волны от частоты или длины волны называется дисперсией, а среда, в которой наблюдается это явление, называется диспергирующей. В диспергирующей среде иесинусоидальный бегущий импульс меняет свою форму в процессе движения, поскольку гармонические волны, входящие в его разложение Фурье, перемещаются с разной скоростью. [17]

Волновая поверхность гармонической волны - од-носвязная поверхность в среде, представляющая собой геометрическое место синфазно колеблющихся точек среды при гармонической бегущей волне. [18]

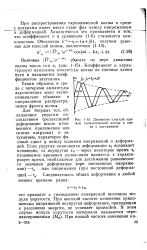Движение плоской прямой гармонической волны в среде с затуханием. [19]

При распространении гармонической волны в среде с потерями имеет место сдвиг фаз между напряжением и деформацией. АнаЖтически это проявляется в тгЖ, что коэффициент v в уравнении ( 1 - 6) становится комплексным. [20]

Фазовая скорость затухающей гармонической волны вводится как отношение реальной части частоты СО к волновому числу А:, т.е. С СО / k, а зависимость СО ( К) называется коэффициентом поглощения. [21]

Рассмотрим дифракцию гармонической волны расширения. [22]

В этом случае падающая гармоническая волна, взаимодействуя с берегами трещины, порождает отраженные волны расширения и сдвига. [23]

Исследование процесса распространения гармонических волн согласно только что изложенной теории показывает, что для волн, длина которых имеет порядок диаметра волокон или расстояния между волокнами, фазовая скорость существенно зависит от длины волны в том случае, когда упругие постоянные армирующего материала значительно отличаются от упругих постоянных матрицы. Следовательно, импульс, распространяющийся в таком материале, будет быстро диспергировать. [24]

Рассмотрим процесс распространения гармонических волн в проводящих средах. [25]

Мы ограничимся рассмотрением только гармонических волн; более сложные волны могут быть представлены совокупностью этих простейших. [26]

Рассмотрим сумму q равных гармонических волн с этими волновыми векторами. Если q 1, 2, 3, 4, 6 ( например, если q - 5), эта сумма не является периодической ( но квазипериодической) функцией. [27]

Исследование скважин методом фильтрационных гармонических волн давления требует специальной аппаратуры, позволяющей создавать гармонические колебания дебита в скважине. [28]

Это выражение описывает гармоническую волну с волновым числом k и частотой о, но с амплитудой, модулированной косинусоидой. [29]

Теплоотдача от вертикальной стенки к стекающей пленке жидкости. Твердая стенка ( у 0 находится при постоянной температуре Ts. Жидкость поступает на стенку при температуре Тй, равномерно распределенной по начальному сечению пленки ( z 0. [30]

Страницы: 1 2 3 4