Нелинейная волна

Cтраница 3

Эволюция кинематических. юли или распределения нефтенасы. [31]

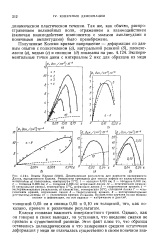
На рис. 8.4.2, д приведены траектории нелинейных волн на ccf - диаграмме, иллюстрирующие развитие описанного процесса. Время t 0 соответствует началу закачки МР, t ti - началу закачки БЖ. После прокачки оэъема жидкости, равного F2Fm ( Vm - поровый объем пласта), происходит образование водо-нефтяного вала. Момент 13 соответствует разрушению оторочки МР. [32]

Существование ( в среде без диссипации) нелинейных волн со стационарным профилем тесно связано с наличием дисперсии. В недиспергйрующей среде учет нелинейности неизбежно нарушает стационарность волны; скорость распространения различных точек профиля оказывается зависящей от значений амплитуды в этих точках, что и приводит к искажению профиля. [33]

Опыты Колски ( 1949. Динамические результаты для варианта эксперимента Данна, выполненного Колски. Результаты приведены для тонких вафель из нижеуказанных материалов. а полиэтилен. температура 21 С. / - толщина 0 025 2 - толщина 0 048 3 - толщина 0 086 4 - толщина 0 268 штриховая линия 10 - статическая кривая. б натуральная резина, температура 17 С, штриховая линия 5 - теоретическая кривая. 6 - экспериментальные результаты. в плексиглас, температура 20 С. сплошная линия 7 - ста-тическая кривая, штриховая линия 8 - теоретическая кривая, 9 - экспериментальные рйэ ьтаты. г медь. 10 - статическая кривая. д свинец. Во всех пяти случаях по оси абсцисс отложр а деформация, по оси ординат - напряжение в дин / см2. [34]

Так же, как обычно, распространением нелинейных волн, отражением и взаимодействием ( включая взаимодействие компонентов с малыми амплитудами и конечными амплитудами) было пренебрежено. [35]

Существование ( в среде без диссипации) нелинейных волн со стационарным профилем тесно связано с наличием дисперсии. В недиспергирующей среде учет нелинейности неизбежно нарушает стационарность волны; скорость распространения различных точек профиля оказывается зависящей от значения амплитуды в этих точках, что и приводит к искажению профиля. Дисперсия же, со своей стороны, приводит к постепенному расплыванию профиля, и оба влияния могут взаимно компенсироваться, приводя к стационарности профиля волны. [36]

Не включена в книгу также и теория нелинейных волн в диспергирующих средах, составляющая в настоящее время значительную главу математической физики. Чисто гидродинамическим объектом этой теории являются волны большой амплитуды на поверхности жидкости. Основные же ее физические применения связаны с физикой плазмы, нелинейной оптикой, различными электродинамическими задачами и др.; в этом смысле она относится к другим томам. [37]

Эта и последующие главы будут посвящены изучению нестационарных нелинейных волн. [38]

О формировании автомодельного решения в задаче о нелинейных волнах в упругом полупространстве, Прикл. [39]

Асимптотическое реше - [ IMAGE ] - 6. Эволюция начального. [40]

Уравнение ( 9 - 49) описывает эволюцию нелинейных волн в дисси-пативной среде и, в отличие от уравнения ( 9 - 42), содержит в качестве решения ударные волны. [41]

Рассмотрим, некоторые приближенные методы расчета коэффициента ослабления нелинейных волн. [42]

В ряде работ рассматривается изменение крутизны переднего фронта, нелинейной волны при ее движении по магнитогидродинамическому каналу - явление, аналогичное опрокидыванию волны Римана ( см., например, С. [43]

Другое плодотворное направление связано с так называемой адиабатической теорией нелинейных волн [7], которая применима в принципе и к сильно диспергирующим волнам произвольной амплитуды. Основные допущения этой теории сводятся к медленности изменения амплитуды, волнового числа и других величин, характеризующих волну на расстояниях и за времена порядка одного периода колебания. В определенном смысле такое приближение представляет собой обобщение теории адиабатических инвариантов в механике. [44]

Перечисленные проблемы представляют значительный интерес для всех разделов физики нелинейных волн; отметим, что во многих физических задачах эффекты статистики поля, статистики среды и статистики распределенных источников проявляются одновременно. [45]

Страницы: 1 2 3 4