Пилообразная волна

Cтраница 4

Отсюда видно, что при Re п ( 1 о) амплитуды гармоник пропорциональны л 1 и одинаково зависят от х, что соответствует формуле (2.25), полученной для разрывной пилообразной волны. [46]

Это, конечно, справедливо не для всех п, а при п Re, где Re aAs / 8oj0, т.е. для частот, малых по сравнению с граничной частотой спектра пилообразной волны, определяемой толщиной ударного фронта. Относительная роль зтих ограничений зависит от числа Рейнольдса для возникающего сателлита Ren аА218ш1: если Ren мало, то ограничение связано с первым условием, а в противоположном случае - со вторым. [47]

Спектрограмма, полученная при дифракции света ( синяя линия ртутного спектра Я 4358 А на ультразвуке частоты 583 кец В воде, a Re - 50, а - 0 7. 6 Ле0 65, а 2 2 ( по Михайлову и Шутилову. [48]

Первая из спектрограмм получена при дифракции на волне, которая еще не превратилась в пилообразную ( форма профиля волны близка к форме, приведенной на рис. 18, б), вторая - на уже сформировавшейся пилообразной волне. [49]

Соответственно остается неизменным отношение толщины ударного фронта к длительности импульса / JoiAx, равное согласно (4.12) ls / l Re 1, так что степень нелинейности плоского импульса при распространении не уменьшается в отличие, скажем, от пилообразной волны. [50]

Как было показано ранее, при больших числах Рейнольдса монохроматическая у источника звука волна переходит в пилообразную. Пилообразная волна является стабильной формой волны конечной амплитуды. [51]

При больших интенсивностях волны накачки она трансформируется в пилообразную волну, возрастает ее поглощение и работа параметрич. Если взаимодействие пилообразных волн происходит в основном в ближней зоне ( цилиндрич. [52]

При а 0 пилообразная волна не успевает образоваться до фокуса, при а О она образуется до фокуса и необходимо принимать во внимание сильное затухание пилообразной волны. [53]

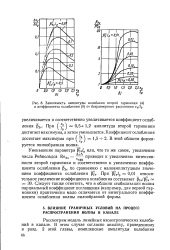Зависимость амплитуды колебания второй гармоники ( а и коэффициента ослабления ( б от безразмерного расстояния 0 / / р. [54]

При ( - J 0 5 - 1 2 амплитуда второй гармоники достигает максимума, а затем уменьшается. В этой области формируется пилообразная волна. [55]

Из (3.22) следует, что уменьшение амплитуды скорости или затухание пилообразной волны не зависит от диссипативных коэффициентов ( вязкости и теплопроводности) среды. Это обстоятельство характерно для пилообразной волны, хотя в конечном счете потеря энергии обусловлена диссипацией при переходе через разрыв. [56]

Следует отметить, что измерения поглощения в [55] проведены при числах Рейнояьдса р / Ьв) - 104 - Н105, так что здесь можно было ожидать увеличения коэффициента поглощения на четыре-пять порядков по сравнению с коэффициентом поглощения волны малой амплитуды, что действительно и наблюдается. Ввиду трудностей измерения поглощения пилообразных волн в воздухе ( влияние стенок трубы, трудности измерения абсолютных значений давления и др.) вряд ли следует ожидать согласия теорией лучшего, чем по порядку величины. [57]

Рассмотрим теперь вопрос о том, почему же к уравнениям ( 5), ( 6), согласно которым далекие гармоники, казалось бы, слабо взаимодействуют между собой, нельзя применять соображения об эстафетной передаче энергии по спектру. Дело в том, что в пилообразной волне все гармоники скоррелированы по фазам и все вместе затухают за счет поглощения энергии на ударном фронте. Если пренебречь корреляцией фаз, то приближенно можно было бы говорить о передаче энергии по спектру, но при этом для каждой гармоники нужно было бы учесть эффект прямого поглощения энергии за счет переноса данной гармоники к ударному фронту. [58]

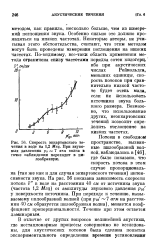Скорость эккартовского течения в воде на 1 2 Мгц. При звуке - Ные пилообразной вол-вых давлениях Р - 7 атм волна в - наблюдались в, точке наблюдения переходит в пи - L J. [59]

На рис. 56 показана зависимость скорости потока v в воде на расстоянии 40 см от источника звука ( частота 1 2 Мгц) oi амплитуды звукового давления рю у поверхности источника. При переходе к течению, вызываемому пилообразной волной ( при рю - 7 атм на расстоянии 40 см образуется пилообразная волна), меняется коэффициент пропорциональности. [60]

Страницы: 1 2 3 4