Рассматриваемая волна

Cтраница 4

Для сравнения на этом же рисунке показано поле бегущей волны того же типа. Картина токов и полей передвигается вдоль оси волновода со скоростью, равной фазовой скорости рассматриваемой волны. [46]

Поскольку в рассматриваемой волне Et 0, a DIUI 0, то электрические граничные условия 3 и 4 в (5.9) автоматически выполняются, и задача об отражении решается как чисто упругая. Точное решение такой задачи, представленное в [24], показывает, что на доменных границах первой группы для рассматриваемой волны отражения нет, а может быть только преломление. Угол преломления ф связан с углом падения ф однозначно. [47]

При этом в (9.114) следует пренебречь первым членом, что приводит к требованию V2a Ca ( 4я2 / 0), характеризующему достаточно малое изменение амплитуды на расстоянии порядка длины волны. Что касается уравнения (9.115), то оно с точностью до постоянного множителя представляет собой закон сохранения энергии, имеющий место при распространении рассматриваемой волны. [48]

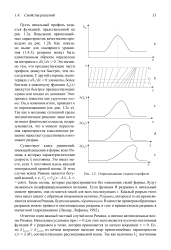Опрокидывание гладкого профиля. [49]

Отметим один важный частный случай волн Римана, а именно автомодельные волны Римана. Если Я л 0 Я л 0, из начала координат выходит веер прямолинейных характеристик x / t Я ( 0), соответствующих рассматриваемой волне. [50]

Эти компоненты, будучи связаны со свойством а2, передают силу, действующую на волну элементарной частицы. Но последняя не описывает собственного состояния а2, поэтому на нее со стороны компонент калибровочного поля, связанных с а2, будут действовать силы, разные для разных собственных состояний а2, образующих рассматриваемую волну. [51]

Эта формула, как и (8.30), содержит в аргументе синусоиды не только время t, но и координату х и, следовательно, является уравнением бегущей волны. В каком направлении перемещается эта волна. Следовательно, рассматриваемая волна напряжения перемещается от конца цепи к ее началу, причем в процессе этого перемещения амплитуда волны убывает. [52]

Множитель я1 / 2 / ( р2 - о2) 4 учитывает затухание амплитуды вдоль прямого отрезка траектории. Фаза состоит из двух слагаемых, первое из которых ( в квадратных скобках) представляет собой задержку луча при движении его по искривленной траектории от края отверстия до точки наблюдения, а второе учитывает отклонение от закона геометрической оптики, возникающее из-за кривизны части траектории. Именно этот фактор объясняет характерную особенность рассматриваемых волн - они экспоненциально затухают при распространении вдоль поверхности цилиндра, причем чем больше я, тем сильнее это затухание в соответствии со значениями хп [ ср. Их свойства мы рассмотрим снова в разд. [53]

Для заданного состояния перед волной Римана или ударной волной, состояние за этой волной принадлежит определенной кривой в пространстве Ut, а именно интегральной кривой волны Римана или ударной адиабате. Для того чтобы определить изменение всех величин в рассматриваемой волне, достаточно определить единственную величину, называемую амплитудой. Нахождение автомодельного решения сводится к соединению точек в пространстве Ut, которые определяют состояния по разные стороны системы волн, используя ломаную линию, состоящую из интегральных кривых расширяющихся волн Римана или ударных адиабат, соответствующих эволюционным разрывам. Действуя таким образом, необходимо удовлетворить неравенствам между скоростями волн: скорость переднего фронта волны, распространяющейся вслед вслед за другой, должна быть не больше скорости заднего фронта предшествующей волны. Решение существует в окрестности определенной точки Uj U, если оно существует в самой этой точке и якобиан dQt [ dUjda ] в ней не равен нулю. Здесь аг - амплитуды волн, которые составляют решение. [54]

Произвольная волна может быть представлена в виде совокупности плоских синусоидальных волн с различными волновыми векторами, частотами, амплитудами и начальными фазами. Такое представление основано на возможности разложения периодической функции в ряд Фурье или выражения непериодической функции с помощью интеграла Фурье ( стр. Совокупность синусоидальных волн, в результате наложения которых получается рассматриваемая волна, называется спектром последней. Совокупность значений амплитуд и частот этих синусоидальных волн называется соответственно спектром амплитуд и спектром частот. [55]

Страницы: 1 2 3 4