Краевая волна
Cтраница 1
Плодотворность метода краевых волн делает актуальным его более строгое математическое обоснование - хотя бы в простейшем случае диффракции на щели. [1]
Поскольку интенсивность краевой волны зависит от периметра частицы, а общая интенсивность рассеянного света пропорциональна площади, отрицательная поляризация в этой модели будет значительной только для маленьких частиц, размером порядка 10 мкм или меньше. Однако не вызывает сомнения, что многие большие объекты также дают отрицательную поляризацию. Например, маленький винт с осью, перпендикулярной плоскости зрения, будет давать отрицательную поляризацию, более четко выраженную, чем лунная; ясно, что эта поляризация обусловлена двойным отражением типа рассмотренного Оманом отражения от резьбы винта, поскольку она исчезает, если резьбу срезать. Вогнутости в зернах лунного грунта или определенные сочетания соседних зерен могут дать такой же результат, как резьба винта. Не исключена возможность, что отрицательная ветвь возникает от взаимодействия одного зерна с лучом света. Волстенкрофт и Роуз [137] показали, что зодиакальный свет также обнаруживает отрицательную поляризацию, хотя частицы в нем, как предполагается, слишком далеки друг от друга, так что многократное отражение или дифракция в сочетании с рассеянием не могут играть важной роли. [2]
В непрерывном режиме возбуждение краевых волн приводит к появлению паразитных боковых лепестков в структуре волнового пучка. Аподизация позволяет видоизменять структуру поля и в этом смысле может рассматриваться как метод обеспечения некоторой фокусировки. Такая возможность часто не учитывается при анализе методов фокусирования ультразвука. [3]
Вычислим ЭПР полосы методом краевых волн [27], полагая длину полосы равной единице. Согласно этому методу отраженное поле формируется регулярной и нерегулярной составляющими наведенного тока. Нерегулярная составляющая тока, локализуемая вблизи ребер и кромок поверхности тела, является источником краевых волн, учет которых необходим при углах незеркальнога отражения. [4]
Особое внимание было уделено исследованию краевых волн типа Кельвина, распространяющихся без затухания в одном из направлений границы бассейна. [5]
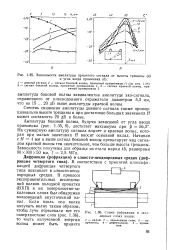 |
Зависимости амплитуды принятого сигнала от высоты трещины ( а и угла ввода приемника ( б. [6] |
На суммарную амплитуду сигнала влияет и краевая волна, которая при малых значениях Н вносит основной вклад. Начиная с Н 4 мм и выше сигнал боковой волны превалирует над сигналом краевой волны тем значительнее, чем больше высота трещины. [7]
По литературным Данным [1552], эхо-импульс краевой волны от верхней кромки наклонно расположенного отражателя ( круглого диска или полосы) имеет отрицательную фазу, и благодаря этому его можно отличить от эхо-импульса от дефекта. [8]
На этом принципе работают циркуляторы на краевых волнах. [9]
Рассмотрим кратко важные для практики свойства и закономерности краевых волн. Свойства остальных дифракционных и объемных волн рассмотрены далее. [11]
При больших углах падения точность можно повысить, применив метод краевых волн [13] или геометрическую теорию дифракции, учитывающие влияние на рассеянное поле волн, дифрагированных на краях отражателя. [12]
Существует несколько методов расчета поля: токовый, апертурный, метод краевых волн, ретроспективный метод расчета. [13]
Эккарт [63], основываясь на теории длинных волн, установил, что краевая волна Стокса является основной среди множества мод, энергия которых поглощается берегом. [14]
В табл. 5.7 приведена схема 14, реализующая амплитудно-временной метод, основанный на использовании дифрагированных краевых волн и волк обегания - соскальзывания. Раздельные излучающий и приемный преобразователи располагают на одной поверхности по обе стороны от обнаруженного дефекта. Сближая их, измеряют время распространения и амплитуду сигнала, дифрагированного на верхнем кончике трещины, или сигнала, отраженного от округлого дефекта. [15]
Страницы: 1 2 3 4
