Спиральная волна
Cтраница 1
 |
Спиральная волна в модели Винера-Розенблюта. [1] |
Спиральная волна для модели Винера-Розенблюта показана на рис. 1.23. Мы видим, что здесь ядро спиральной волны ( покоящаяся область в ее центре) вообще отсутствует. [2]
 |
Траектория движения кончика спиральной волны при двух различных соотношениях между частотой модуляции и собственной частотой спиральной волны ( численный расчет B.C. Зыкова. [3] |
Резонанс спиральных волн наблюдается в эксперименте [2] с использованием светочувствительной модификации реакции Белоусова - Жабо-тинского, катализатором в которой являлось соединение рутения. В среде первоначально создавали спиральную волну или пару таких волн. Затем, после измерения периода установившегося вращения спиральной волны, раствор начинали периодически однородно освещать с помощью интенсивного источника. [4]
Топологический заряд спиральной волны в двумерной среде равен деленному на 2тг изменению фазы при обходе по направлению часовой стрелки вдоль замкнутого контура, окружающего ядро спиральной волны. [5]
Об устойчивости спиральных волн свидетельствуют данные многочисленных экспериментов и результаты численных расчетов. [6]
При обсуждении свойств спиральных волн в разд. В отличие от этого ведущие центры не обладают какой-либо определенной частотой. В одной и той же среде могут наблюдаться ведущие центры с разными размерами центральной области, а следовательно, с различными частотами. Каким будет временной период ведущего центра - зависит от вида начального воздействия, приведшего к его образованию. [7]
Этим определяется частота вращения спиральной волны. Поскольку дифференциальные уравнения ( 3) и ( 4) не допускают полного аналитического решения, для нахождения величины со, а также функций р ( г) и ( г) приходится прибегать к приближенным методам. [8]
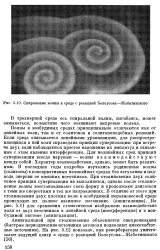 |
Спиральные волны в среде с реакцией Белоусова-Жаботинского. [9] |
В трехмерной среде ось спиральной волны, изгибаясь, может замыкаться, вследствие чего возникают вихревые кольца. [10]
 |
Период однорукавной спиральной волны ( кривые 1, 3 и минимальный возможный период следования импульсов ( кривая 2 как функции параметра а, характеризующего возбудимость среды. [11] |
Полученная простая оценка частоты спиральной волны и радиуса ее ядра оказывается довольно близкой к действительности в случае хорошо возбудимых сред ( ср. Причина такого расхождения понятна. [12]
Между тем, участки спиральной волны, лежащие ближе всего к ядру, имеют большую кривизну и, следовательно, должны двигаться несколько медленнее одиночного импульса. В результате частота циркуляции спиральной волны уменьшается по сравнению со значением сотах. [13]
Определим теперь знак энергии квазистационарной спиральной волны. [14]
Полученный результат позволяет доказать неустойчивость спиральной волны для ограниченной области, имеющей в сечении форму квадрата. В самом деле, эту квадратную область можно продолжить до бесконечной решетки; при этом решения в двух соседних областях получаются одно из другого преобразованием зеркальной симметрии, т.е. направления вращения спиральных волн в соседних ячейках противоположны, вследствие чего вся эта система стремится аннигилировать. Аналогичное рассуждение доказывает неустойчивость отдельной спиральной волны в области, имеющей в сечении форму правильного треугольника. Однако для правильного шестиугольника оно, как легко понять из элементарного рассмотрения, уже не подходит. Это означает, что спиральные волны могут образовывать на плоскости устойчивую гексагональную решетку. [15]
Страницы: 1 2 3 4 5