Спиральная волна
Cтраница 3
 |
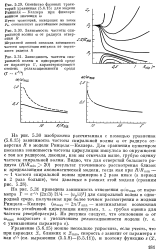
Ведущие центры.| Схема образования ревербератора из разрыва фронта волны. [31] |
При разрыве волнового фронта может возникать ревербератор - спиральная волна. [32]
 |
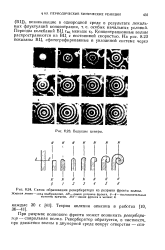
Рассчитанные на ЭВМ зависимости периода спиральной волны Т ( 1 и минимального периода следования импульсов Тш ( 2 от параметра к, характеризующего наклон средней ветви 5-образной изоклины. [33] |
В работе [70] проведено более детальное рассмотрение структуры спиральной волны, значительно улучшающее выводы простого геометрического анализа. Основная идея, использованная в этой работе, состояла в переходе к новым координатам, в которых фронт спиральной волны оказывается выпрямленным и задача сводится к циркуляции импульсов по системе окружностей в некоторой эффективной среде, свойства которой зависят от удаления от центра спирали. Введем новый полярный угол г) - ф % ( г), отсчитываемый от фронта спиральной волны, так что в координатах r, i) спираль оказывается выпрямленной по радиальный луч. [34]
Поскольку они имеют круговую поляризацию, их называют спиральными волнами, или геликонами. [35]
При высокой инерционности ( y / D 1) спиральная волна смещается вдоль оси л: в направлении, обратном направлению увеличения Ккр. Если инерционность мала ( y / D 1), дрейф осуществляется вдоль осну, при этом его направление меняется на обратное при изменении направления вращения спиральной волны. [36]
Они выполняются, если возбудимость среды достаточна для существования спиральных волн, но все же не слишком высока. [37]
Как видно, при Ккр - 0 частота вращения спиральной волны со0 убывает и стремится к нулю; при этом радиус RQ ядра спиральной волны неограниченно возрастает. [38]
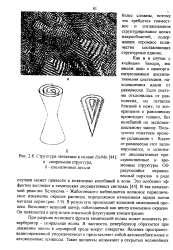 |
Структура эвтектики в сплаве Zn-Mn. [39] |
При разрыве волнового фронта химической волны может возникать ревербератор - спиральная волна. В частности, ревербератор образуется при движении волны в двумерной среде вокруг отверстия. Явления пространственно-временной упорядоченности представляют собой автоколебательные и автоволновыс процессы. [40]
Заметим, что характерное время релаксации возмущения формы фронта TD спиральной волны всегда мало по сравнению с ее периодом циркуляции. [41]
Следовательно, задача о дрейфе сводится к задаче о резонансе спиральной волны при точном совпадении частот. [42]
В последние годы многомерные задачи для таких систем связывают со спиральными волнами, в частности спиральными волнами на сердце, попытками объяснить явления фибрилляции и др. Традиционной областью исследования волновых процессов являются задачи горения. В последние годы в физике горения возникают все новые и новые интереснейшие модели распространения волн. Среди них, в частности, можно указать спиновые режимы, когда очаги движутся по спирали па повцрхности цилиндра, периодические по времени многомерные режимы и др. Наконец, отметим также важные для химической кинетики модели распространения концентрационных волн. Эти и ряд других задач физики, химии и биологии ( с некоторыми ия них можно познакомиться по обзору [8] и сборнику статей [1]) и определяют все возрастающий интерес к изучению волновых решений параболических уравнений, основы которого были заложены в работе КПП. [43]
На рис. 5.30 изображена рассчитанная с помощью уравнения (5.6.15) зависимость частоты спиральной волны ш от радиуса отверстия R в модели Ринцеля-Келлера. Для сравнения пунктиром показана зависимость частоты циркуляции импульса по окружности с тем же радиусом, дающая, как мы отмечали выше, грубую оценку частоты спиральной волны. [45]
Страницы: 1 2 3 4 5