Регулярный волновод

Cтраница 4

Таким образом, для определения коэффициента связи по формуле (3.3.3) необходимо знать поля собственных волн на границе раздела в регулярном волноводе сравнения ( § 3.1) и функцию ст ( s), характеризующую отклонение реального волновода в данном поперечном сечении от регулярного волновода. Естественно что для регулярного волновода а 0 и, стало быть, коэффициенты связи SjV также равны нулю. [46]

Сравнительный анализ фазочастотных зависимостей для элементов матрицы рассеяния тройников ( рис. 142, б и 139, в) приводит к выводу, что для Я-плоскостных тройников функции argSf / x) изменяются значительно быстрее с увеличением частоты ( плоскости отсчета arg Si / и argS oo совпадают с апертурами регулярных волноводов) и в большем интервале значений. [47]

Таким образом, каждая из упомянутых волн может существовать в отдельности и независимо от существования других типов волн. Другими словами, теория регулярного волновода не может дать ответа на вопрос о том, какие же типы волн и в каких амплитудных соотношениях имеются в действительности. Неопределенность решения задачи здесь вызвана тем, что граничные условия были заданы лишь частично, а именно на регулярной боковой поверхности волновода. [49]

Рассмотрим случай идеальной проводимости боковой поверхности R. В этом случае в регулярном волноводе существует счетная система нормальных волн, которая распадается на две подсистемы ТЕ - и ГМ-волн. [50]

Нормальные волны в регулярном волноводе являются естественным базисом для представления любого решения однородной системы уравнений Максвелла. Для любого электромагнитного поля в регулярном волноводе справедлива следующая теорема о представимости его в виде суперпозиции ТЕ - и ТМ-волн. [51]

Во все формулы § 12, характеризующие статистические свойства потерь Qj ( z, К) и дополнительного набега фазы ( pi ] ( z, К) [ за исключением формулы (12.16) ], входит лишь один обобщающий Статистический параметр - среднее значение QJZ потерь на преобразование рабочей волны в / - ю паразитную. Остальные параметры в этих формулах являются параметрами регулярного волновода. [52]

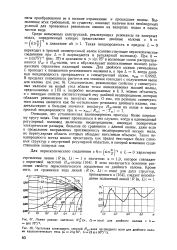Линии равных значений U7j ( sin 750 - 1.| Частотная зависимость энергий Я10 - волн прошедшего поля для двойного излома квазиоптического типа ( Z, 2tg60, h ( 2 sin 600 1. [53]

Очевидно, что установленная закономерность присуща более широкому кругу задач. Она может проявляться в тех случаях, когда в одномодовый регулярный волновод включены неоднородности, имеющие поперечные электрические размеры, большие по сравнению с длиной волны, даже если в продольном направлении протяженность неоднородностей весьма мала, но нерегулярная область которых обладает ненулевым объемом. Такие неоднородности всегда можно представить как предел некоторых более сложных структур с внутренней регулярной областью, в которой возможно существование запертых мод. [54]

К простейшим неоднородностям координатно-плоскостного типа относятся ступенчатые сочленения волноводов разных поперечных сечений, бесконечно тонкие диафрагмы, диафрагмы конечной толщины и пр. В отличие от уголковых ступенчатые неоднородности не изменяют направление оси тракта, отдельные регулярные волноводы непосредственно примыкают друг к другу, что значительно упрощает решение соответствующих краевых задач дифракции. Количество публикаций, посвященных анализу свойств этих неодно-родностей в круглых, прямоугольных и плоскопараллельных волноводах, весьма велико и труднообозримо. [55]

Для некоторых конструкций устройств используется связь ДР одновременно с регулярным и запредельным волноводами. При: этом наличие отрезка запредельного волновода приводит к уменьшению амплитуды поля регулярного волновода в месте расположения ДР и, следовательно, к уменьшению его связи с регулярным волноводом. Электродинамический расчет связи в такой: структуре сложен, поэтому в ряде случаев можно воспользоваться экспериментальным нахождением коэффициентов связи или. В этой работе были проведены эксперименты по определению степени обусловленного влиянием запредельного волновода уменьшения амплитуды магнитного поля / гв прямоугольного регулярного волновода. [56]

Страницы: 1 2 3 4