Уединенные волны

Cтраница 3

Тогда такая уединенная волна называется солитоном. Другими словами, солитонами являются те уединенные волны, профили плотностей энергии которых асимптотически ( при t - оо) возвращаются к своим первоначальным формам и скоростям. Векторы 6г описывают возможность твердого перемещения солитонов с их первоначальных траекторий. Для солитонов такое перемещение является единственным остаточным эффектом столкновений. Очевидно, что это - замечательное свойство решений нелинейных полевых уравнений. [31]

Уединенные волны могут быть использованы для барообработки тяжелых нефтей о целы) улучшения их термогидродинамических свойств, для передачи динамических импульсов на больше расстояния в гидравлических системах, например, о устья на призабойную зону скважины. Кроме того, как видно из рисунка уединенные волны могут значительно превосходить имитвругадай гидравлические удар, что необходимо учитывать для предотвращения осложнений в соответствующих технологических системах. [32]

По нашему мнению, понятие солитона и в самом деле целесообразно расширить. Так, в последнее время были рассмотрены уединенные волны, которые в результате взаимодействия сохраняют свою структуру как частицы, но не расходятся, а, напротив, образуют связанную пару; такие уединенные волны естественно так ке назьшать солитрнами. [33]

Ясно, что при этом влияние ненулевой начальной температуры на профиль ударной волны, которое может оказаться существенным, остается неисследованным. В частности, неизвестно, существуют ли по-прежнему уединенные волны, с которыми связаны нестационарность ударной волны и отсутствие равновесия за ее фронтом, если начальные условия для атомов в цепочке имеют случайный характер. Если это так, то вероятность того, что и в реальных кристаллах при ударном сжатии возникают солитоны, значительно возрастает. [34]

Поскольку в цепочке происходят столкновения между уединенными волнами, интересно исследовать их устойчивость при этих столкновениях. Около 170 - й частицы в цепочке мы наблюдаем две уединенные волны, распространяющиеся независимо друг от друга и хорошо разделенные во времени, причем движущаяся быстрее волна большей амплитуды находится позади. К тому времени, когда они достигнут 185 - й частицы, уединенная волна большей амплитуды догоняет меньшую и происходит их нелинейное взаимодействие. Когда пара волн достигает 200 - й частицы, мы обнаруживаем, что быстро движущаяся уединенная волна полностью прошла сквозь медленно движущуюся, но каждая из них сохранила свою первоначальную форму. [35]

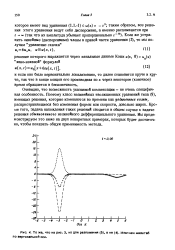То же, что на 3, но для разложения ( 5, а не ( 4. Изменен масштаб по вертикальной оси. [36]

Очевидно, что возможность указанной компенсации - не очень специфичная особенность. Поэтому класс нелинейных эволюционных уравнений типа ( 9), имеющих решения, которые изменяются во времени как уединенные волны, распространяющиеся без изменения формы или скорости, довольно широк. Кроме того, задача нахождения таких решений сводится в общем случае к задаче решения обыкновенного нелинейного дифференциального уравнения. Мы продемонстрируем это ниже на двух конкретных примерах, которых будет достаточно, чтобы показать общую применимость метода. [37]

Важно понимать, что большинство нелинейных уравнений в частных производных, обладающих решениями в виде уединенных волн, не имеют решений, ведущих себя как солитоны. Некоторые из таких уравнений имеют решения, ведущие себя почти как солитоны в том смысле, что когда две уединенных волны встречаются, то после столкновения они возрождаются с малыми изменениями профиля, и лишь малое количество энергии теряется при этом в виде последующих колебаний. Такое поведение часто называют солитоноподобным, или говорится, что столкновение уединенных волн демонстрирует неупругое солитонное поведение. [38]

Очевидно, что полученные выше результаты нахо-дятся в противоречии с обычными допущениями, принятыми при континуальном рассмотрении ударного сжатия. Во-первых, профиль ударной волны нестационарен во времени, поскольку скорости импульсов позади фронта изменяются по мере их превращения в уединенные волны. Следовательно, за фронтом ударной волны температура не возрастает. В § 4 мы увидим, как модифицируется это аномальное поведение под влиянием ненулевой начальной температуры в цепочке. [39]

Забуски и Крускал назвали эти уединенные волны солитонами именно потому, что когда две или больше уединенных волны КдФ сталкиваются, то они не разрушаются и не рассеиваются. Греческое окончание - он обычно используется для частиц, и поэтому слово солитон призвано как бы подчеркнуть тот факт, что уединенные волны ведут себя подобно частицам. [40]

Прежде всего обе модели были опробованы на задаче о бегущем над ровным дном соли-тоне. Расчеты показали, что, здесь, как и в случае дискретных моделей меньшей размерности, даже на достаточно грубой сетке реализуются уединенные волны, которые в силу консервативности дискретной модели и численного алгоритма распространяются с постоянной средней амплитудой, энергией и фазовой скоростью. [41]

Конечно, сумма двух локализованных решений типа ( 14) [ с соотношениями ( 16) и ( 20); параметр р может принимать два различных значения для этих двух решений ] дает приближенное решение уравнения ( 19), пока они локализованы далеко друг от друга, так что их перекрыванием можно пренебречь. Но теперь уже нельзя сказать, что решение, первоначально заданное в виде суммы двух удаленных друг от друга уединенных волн, движущихся с разными скоростями, после их сближения даст в отдаленном будущем сумму тех же уединенных волн; теперь происходит как бы неупругое столкновение уединенных волн, при котором могут измениться их свойства и возникнуть другие уединенные волны с выделением излишка в виде диспергирующей части. [43]

Уединенные волны - это стационарные импульсы ( волновые пакеты), распространяющиеся в нелинейной среде с дисперсией. Они сохраняют свою форму благодаря динамическому балансу между нелинейностью и дисперсией. Солитоны - это особые уединенные волны, которые сохраняют свою форму даже при столкновениях друг с другом. В плазме, вообще говоря, существует много нормальных волн, соответствующих различным типам дисперсионных зависимостей. В ходе широких исследований волн в плазме, проводившихся в последнее десятилетие, были выявлены разнообразные механизмы нелинейности. [44]

За прошедшие годы ситуация резко изменилась. Солитоны в магнетиках, уединенные волны, аттракторы, точки бифуркации - все это встречается в работах по физике твердого тела не менее часто, чем привычные магноны, фононы и электроны проводимости. Исследованию нелинейных свойств твердых тел посвящено множество работ. Поскольку постепенно было выяснено, что нелинейные задачи, как и линейные, обладают большой общностью ( в какой-то мере они потеряли свой индивидуализм), то обнаружилось ранее неизвестное сходство - скажем, в поведении системы параметрически возбужденных магнонов и определенных экосистем. [45]

Страницы: 1 2 3 4