Уединенные волны

Cтраница 2

Однако решениями уравнения ( 53) являются только кноидальные и уединенные волны, и - нег никаких решений, которые могли бы удовлетворить граничным условиям, необходимым для существования ударного фронта. [16]

Видно, что данная модель дает возможность получать хорошие уединенные волны на весьма грубой с точки зрения других численных методов ( ср. [17]

Рассмотрим прежде всего стационарные решения этой системы, описывающие уединенные волны. [18]

Забуски и Крускал назвали эти уединенные волны солитонами именно потому, что когда две или больше уединенных волны КдФ сталкиваются, то они не разрушаются и не рассеиваются. Греческое окончание - он обычно используется для частиц, и поэтому слово солитон призвано как бы подчеркнуть тот факт, что уединенные волны ведут себя подобно частицам. [19]

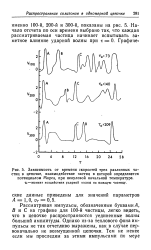Зависимость от времени скоростей трех различных частиц в цепочке, взаимодействие частиц в которой определяется потенциалом Морса, при ненулевой начальной температуре. [20]

Рассматривая импульсы, обозначенные буквами Л, В и С на графике для 100 - й частицы, легко видеть, что в цепочке распространяются уединенные волны большой амплитуды. Однако из-за теплового фона импульсы не так отчетливо выражены, как в случае первоначально не возмущенной цепочки. [21]

Следовательно, имеются только два решения ( в виде непрерывных волн), не равные всюду константе, - это кноидальные волны в случае А и уединенные волны в случае В. [22]

Четко определив различие между солитонами и уединенными волнами ( первые являются узким подклассом последних), необходимо заметить, что в большей части литературы оно затушевывается. Уединенные волны часто называют солитонами, по-видимому, потому, что последнее название более ясно и привлекательно. В последующих главах мы тоже поддадимся популярной тенденции использовать название солитон для уединенных волн. Но по крайней мере в этой главе различие будет сохранено. [23]

Отметим, что (2.8) определяет уединенные волны с числом пространственных измерений от одного и выше. Многие уединенные волны, которые мы будем обсуждать, получаются как статические решения. [24]

Фазовые кривые для уравнения ( ср. с. [25]

Таким образом, уединенные волны, распространяющиеся поперек магнитного поля в холодной плазме, имеют предельное значение числа Маха и соответственно амплитуды. [26]

Это решение тривиально, и, таким образом, теорема запрещает нетривиальные изменяющиеся в пространстве решения. Зависящие от времени уединенные волны могут существовать для скалярных полей в ( D 1) измерениях даже при D 3 ( гл. Но теорема указывает, что при поиске статических решений в реальном мире ( 3 1) измерений необходимо рассматривать модели, состоящие не только из одних скалярных полей. Но прежде полезно рассмотреть более простую модель, чтобы получить представление о некоторых важных идеях, которые потребуются в последующих разделах. Эта система состоит только из скалярных полей, но в ( 2 1) измерениях. [27]

Результаты численных расчетов свидетельствуют о том, что, несмотря на формально первый порядок аппроксимации, описанная модель обеспечивает хорошее качество расчетов. Она дает возможность получать хорошие уединенные волны на весьма грубой с точки зрения других численных методов сетке. Немаловажным является также то, что в данной модели получаются настоящие уединенные волны, т.е. незатухающие одиночные возмущения определенной формы, распространяющиеся с постоянной скоростью. [28]

Однако такое заключение справедливо лишь для волн, описываемых линейными уравнениями. Для нелинейных волн ситуация другая-возможны уединенные волны ( солито-ны), которые пространственно сосредоточены в малой области пространства и распространяются без изменения своей формы и размеров. Хотя солитоны были открыты более 100 лет назад, особенно большой интерес возник к ним в настоящее время в связи с решением некоторых задач квантовой механики. Затем солитон-ные решения были найдены во многих явлениях, описываемых нелинейными дифференциальными уравнениями. Солитоны также рассматривались в качестве кандидатов на роль частиц. Однако достаточно удовлетворительных результатов в этом направлении не получено. [29]

Колебания), однако возможны и уединенные волны в виде локализованных в пространстве импульсных возмущений ( взрывные В. [30]

Страницы: 1 2 3 4