А-поле

Cтраница 1

А-поля подразделяются на on, off и смешанные on - off типы. On-поля реагируют на увеличение, off - поля - на уменьшение световых воздействий. Смешанные on - off поля объединяют оба эффекта. [1]

Любое а-поле является монотонным полем, и наоборот. [2]

Множества из а-поля, порожденного элементарной функцией, измеримы. [3]

Следовательно, наиболее грубое достаточное а-поле cZ0 является минимальным. [4]

Пусть есть а-поле подмножеств пространства X. X, что фх ( х) ф2 ( А:), принадлежит идеалу А. Мы говорим тогда, что функции фх и ф2 являются / - эквивалентными, или просто эквивалентными. Эта процедура производится, например, в теории меры и интегрирования, причем А является а-идеалом множеств меры нуль. [5]

Прообраз а-поля есть а-поле прообраз минимального о-поля, порожденного некоторым классом, является минимальным а-полем, порожденным прообразом этого класса; класс всех множеств, прообразы которых принадлежат к некоторому о-полю, является о-полем. [6]

Заметим, что а-поле [ / о, s ] единственно и содержит полную информацию о поведении случайного процесса Xt в прошлом. [7]

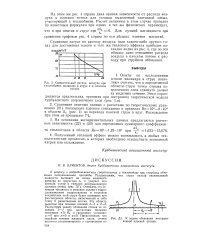Сравнительный расход воздуха при. [8]

Опыты по исследованию а-поля цилиндра в струе позволяют считать, что в определенной области струи точка отрыва пограничного слоя сдвинута далеко за миделево сечение. [9]

Множества, принадлежащие а-полю & с индексами или без индексов, будем обозначать В с теми же самыми индексами, если они есть. [10]

Действительно, пусть есть а-поле всех борелевских подмножеств единичного интервала f /, л - лебегова мера на г, а А - а-идеал всех множеств ( поля), мера л которых равна нулю. [11]

Отсюда следует, что а-поле & ( XTS) составляется из а-полей ( Х (), а теорема В превращается в следующую теорему. [12]

Если ф, определенная на а-поле % а-аддитивна ( и значение - оо исключено), то ф ограничена снизу. [13]

Если дана мера ц на а-поле, то всегда возможно продолжить ц на более обширное а-поле. [14]

Мы говорим при данном ( а-поле) 4 а не при данном ( разбиении) В. [15]

Страницы: 1 2 3 4