Координатный базис

Cтраница 1

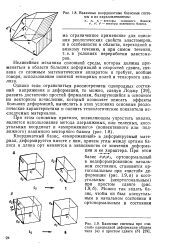Взаимные координатные базисные системы и их параллелепипеды.| Базисные системы при чистой однородной деформации общего типа ( а и простом сдвиге ( б. [1]

Координатный базис, вмороженный в деформируемый материал, деформируется вместе с ним, причем углы между ортами базиса и длина орт меняются в зависимости от значения деформации и ее характера. [2]

Координатный базис нашей задачи выберем так, чтобы поперечные оси лежали в плоскости и перпендикулярно плоскости рисунка. [3]

О координатном базисе моделей макроуровня подробнее будет сказано в последующих разделах. Здесь же отметим, что в механике фазовые координаты типа потока выбирают в качестве обобщенных координат. Количество независимых обобщенных координат системы равно числу ее ступеней свободы. [4]

Целесообразнее изменить координатный базис путем введения геометрических координат Х ( вместо фазовых координат Fyj и осуществить замену дифференциальных уравнений относительно производных dFyj / dt уравнениями вида dxi / dt Uj. В этом случае функции усилий в упругих элементах Fyj будут вычисляться через координаты х, которые, так же как и координаты Vi, относятся к переменным типа потока. [5]

Как строится локальный координатный базис. [6]

Благодаря использованию полного координатного базиса, отождествленного с множеством токов и напряжений всех ветвей схемы, строгий приоритет ветвей при выборе фундаментального дерева, свойственный уравнениям переменных состояния, утрачивает свое прежнее значение, и при выборе дерева руководствуются лишь степенью разреженности матрицы. Максимальной разреженности матрицы схемы в (4.301) можно достичь лишь за счет ее топологической части, так как разреженность ее компонентной части зависит только от числа и типов схемных двухполюсников. В работе [221] рассмотрен алгоритм получения максимально разреженной матрицы л, основанный на выборе дерева в порядке убывания веса ветвей, оцениваемого суммарной кратностью инцидентных ей вершин. [7]

Схема к примеру формирования уравнений равновесия. [8]

Однородные ( канонические) координатные базисы указанных типов используются в тех случаях, когда искомыми переменными при численном анализе модели являются соответственно только токи или напряжения, причем компонентные уравнения должны допускать описание всех компонентов в первом случае для токов, а во втором - для напряжений. [9]

Сходимость результатов в зависимости от размерности координатного базиса улучшается с увеличением зоны приложения локальной нагрузки. [10]

В качестве примера формирования уравнений в расширенном каноническом координатном базисе, обладающего общностью полного координатного базиса без предварительного выбора дерева, рассмотрим схему инвертора, приведенную на рис. 1.45 а. Эквивалентная схема инвертора ( рис. 1.45 6) содержит шесть узлов, кроме базисного, и пять особых компонентов ( Ei, Ег, Е3, / f сЫ э, / 2а / Гк), поэтому матрица в расширенном координатном базисе будет иметь порядок 11 ХП. [11]

Табличный метод иногда называют методом моделирования в полном координатном базисе. Полный координатный базис, так же как и обобщенный, избыточный; из него без ущерба для общности можно исключить величины постоянные или переменные, зависящие только от времени. В результате сокращается размерность ММС. Переменные, зависящие от времени, принадлежат источникам типа Е и I. При выборе дерева необходимо обеспечить попадание ветвей источников типа Е в дерево, а ветвей источников типа I - в хорды. При этом 1Е для источников типа Е и U, для источников типа I входят в координатный базис. Из ММС исключаются компонентные уравнения таких источников, а переменные 1Е и U, будут найдены из топологических уравнений. [12]

Величина ( i также не зависит от выбора координатного базиса. [13]

Эти соотношения выражают необходимые и достаточные условия голономности координатного базиса ег. [14]

Выписанную тройку векторов называют нормально связанным с поверхностью основным координатным базисом. [15]

Страницы: 1 2 3 4