Эквивалентная матрица

Cтраница 2

Таким образом, для любой порождающей матрицы G существует эквивалентная матрица G, которая, если не принимать во внимание расположение информационных символов, соответствует систематическому коду. Проверочная матрица Н для эквивалентного систематического кода имеет вид, аналогичный представленному на рис. 6.1.3, с той разницей, что единичная подматрица занимает те - ( N-L) строк, которые соответствуют положению проверочных символов, и эти строки не обязательно являются последними N-L строками. Синдром принятой последовательности у, как и прежде, определяется равенством S уЯ и можно, как и прежде, проводить декодирование на основе синдромной таблицы декодирования. [16]

Расчет и оптимизация ХТС с помощью операционных матриц заключается в составлении эквивалентной матрицы. [17]

ЗАМЕЧАНИЕ 1.1. Из доказанной теоремы следует, что в любом классе эквивалентных матриц существует хотя бы одна, имеющая каноническую диагональную форму. Однако справедлива теорема единственности. [18]

При данном х и при разных ft выражение ( 13) дает эквивалентные матрицы. [19]

У о - вектор-столбец выходных переменных системы; [ С ] - эквивалентная матрица преобразования ХТС, элементы которой представляют собой функции элементов операционных матриц, или матриц преобразования отдельных ТО; символ - транспонирование матрицы. [20]

При умножении любой матрицы на невырожденные матрицы ее ранг не меняется, поэтому эквивалентные матрицы имеют одинаковые ранги. Пусть теперь две матрицы одинаковых размеров имеют один и тот же ранг. Докажем, что эти матрицы эквивалентны. [21]

При решении задач анализа ХТС структурные блок-схемы позволяют определить эквивалентный коэффициент передачи ( или эквивалентную матрицу преобразования) системы в целом. [22]

Если бы мы взяли вращения вокруг оси х или у, то пришли бы к эквивалентным матрицам / lt / 2, имеющим те же собственные значения; но в § 9 базис спин-тензорного представления был выбран таким образом, что / з представляется проще. [23]

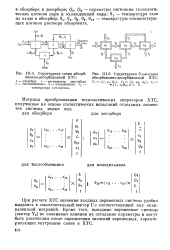Структурная схема абсорб-ционно-десорбционной ХТС.| Структурная блок-схема абсорбционно-десорбционной ХТС. [24]

При расчете ХТС значения входных переменных системы удобно выделить в самостоятельный вектор U с соответствующей ему эквивалентной матрицей. Кроме того, выходные переменные системы ( вектор Y0) не оказывают влияния на остальные параметры и могут быть рассчитаны после определения значений переменных, характеризующих внутренние связи в ХТС. [25]

Заметим, что из совпадения у всех эквивалентных матриц многочленов Dk ( Я) следует, что эквивалентные матрицы имеют один и тот же ранг. [26]

Для расчетов в статических и динамических режимах коэффициентов передач или функциональных связей между переменными математической модели ХТС, представленной в виде эквивалентной матрицы преобразования ( 11 11), а также для определения количественных оценок характеристик чувствительности л устойчивости систем необходимо использовать алгоритмы решения сигнальных графов. [27]

Задачи выбора, определяемые эквивалентными матрицами, являются эквивалентными, так как можно доказать, что множества оптимальных назначений двух задач выбора с эквивалентными матрицами совпадают. [28]

Мы не будем давать доказательства этого утверждения, так как оно требует долгих рассуждений алгебраического характера, сходных с используемыми при выводе канонической формы Смита для эквивалентных матриц, являющихся полиномами от К. Здесь встретятся дополнительные трудности, так как матрицы содержат также экспоненты по X. [29]

Если матрицы Аи В имеют размер т х гг, то в ( 32) квадратная матрица Р имеет порядок т, а квадратная матрица Q - порядок гг. Если элементы эквивалентных матриц А и В принадлежат некоторому числовому полю, то матрицы Р и Q могут быть выбраны так, чтобы их элементы принадлежали тому же числовому полю. [30]

Страницы: 1 2 3 4